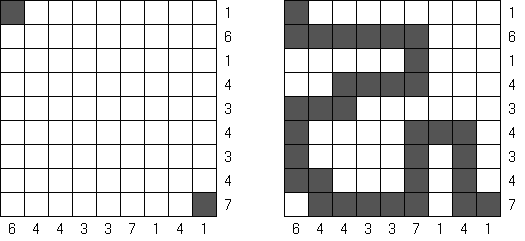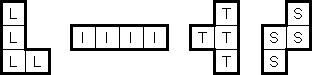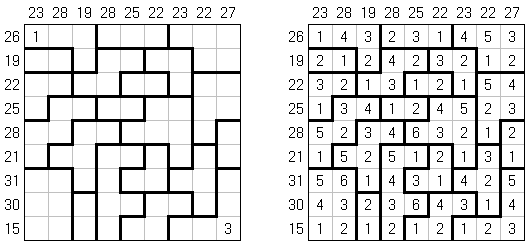|
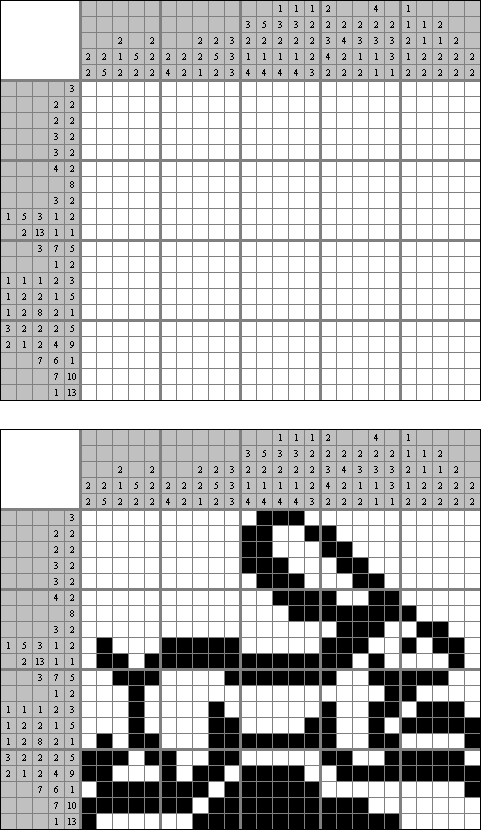
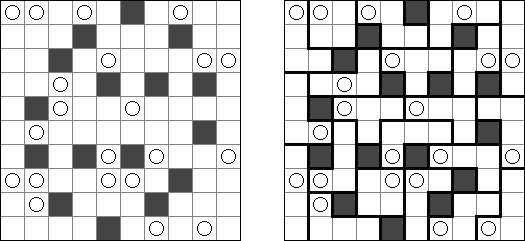
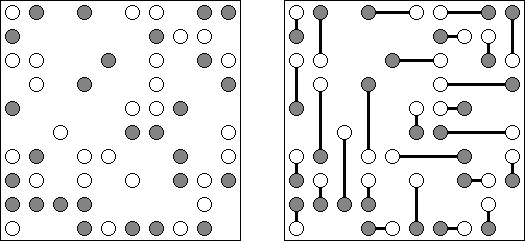
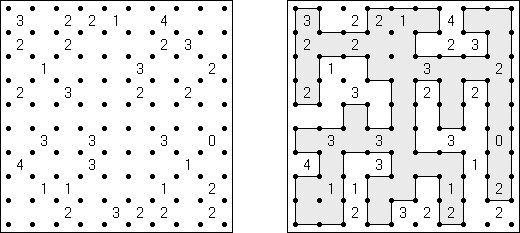
Cross+A  智力游戏 智力游戏Cross+A 软件是一种能解决各种各样谜题的软件。软件支持谜题的成批处理。 逻辑谜题 Nonogram (数图,"Hanjie", "Paint By Numbers", "Griddler","CrossPix") 谜题的盘面是个正方形或长方形,它的目的是根据给出的数字得到一幅妙趣横生的简笔画;左边和上面的数字及其数量指出在相应的线上每个集合的黑色方格数量和黑色方格集合的数量。黑色方格集合中间一定有最少一个空方格。
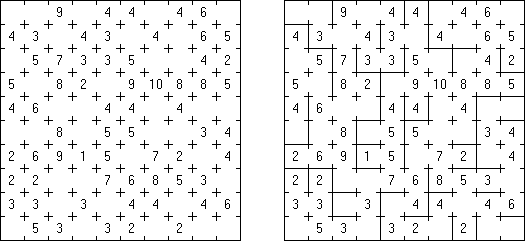
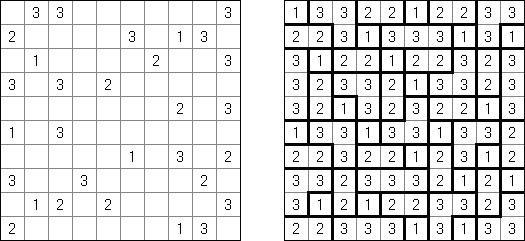
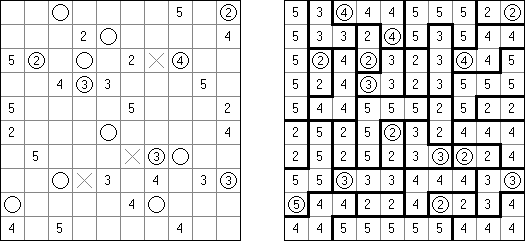
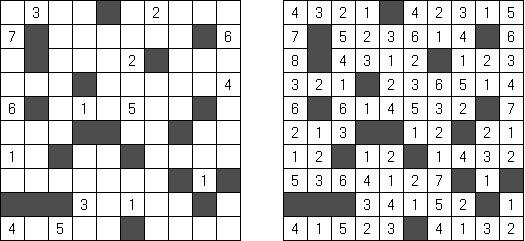
Kakuro (数谜,"Cross Sums") 是一种数字谜题,也是纵横字谜的数学模拟体。需要将1至9数字填入方格中,有的方格无法填上(黑色方格)。在包含数字的黑色方格中上面的数字表示在该方格右边白色方格的数字之和,而在黑色方格中下面的数字表示在该方格下面白色方格的数字之和。比如,"6"数字是1+5 或2+4之和;不得填上同一的数字(3+3)。
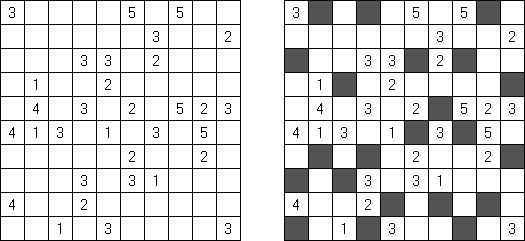
Hitori ("单独")是一种逻辑谜题。需要将重复的数字涂黑,数字在任何行或列里不重复。涂黑的方格只能用格角毗邻,不可以用方格的侧边毗邻。未涂黑的小格要构成连续不断的白色空间,白色方格与白色方格之间必须相连。
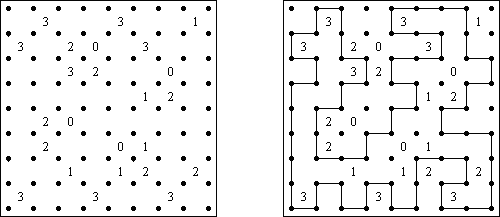
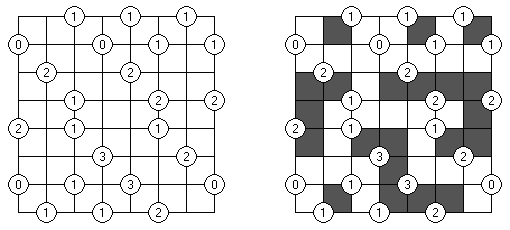
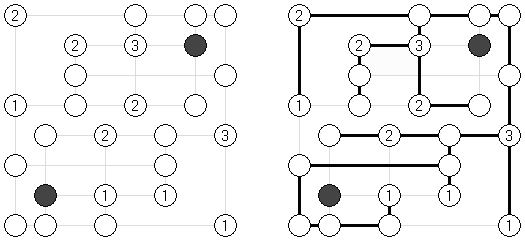
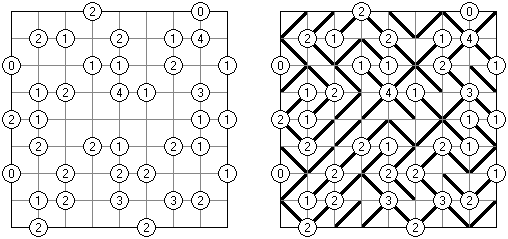
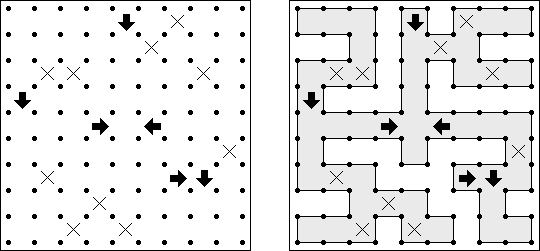
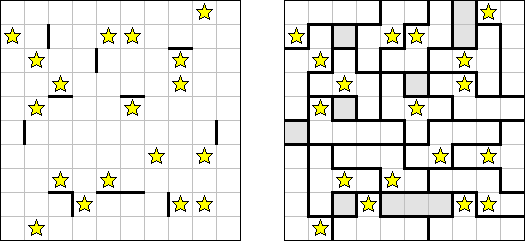
Slitherlink (数回,"Fences", "Loop the Loop", "Dotty Dilemma","Sli-Lin")是一种逻辑谜题,与迷宫相似。需要用纵线段和横线段将圆点连接起来以构成一条不间断而不交叉的回路。每个数字相当于该数字四周的线段数量。如果在方格中没有数字,那么该方格四周的线段数量不限。
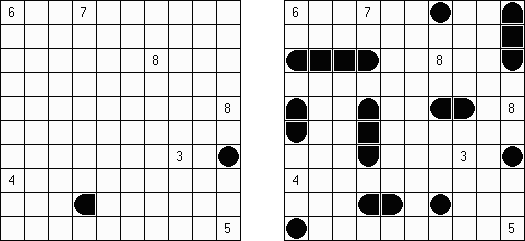
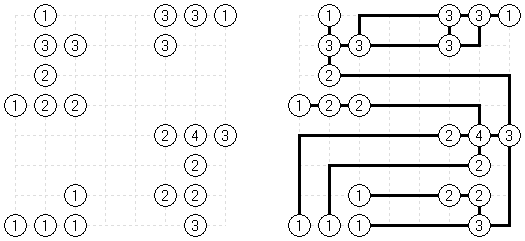
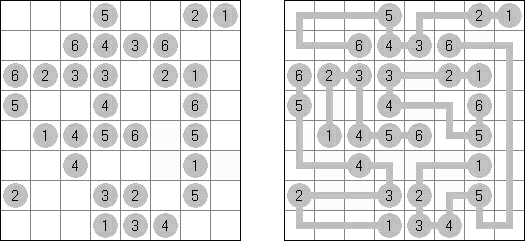
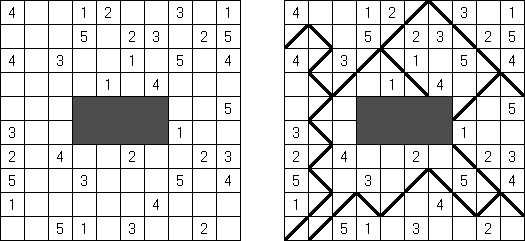
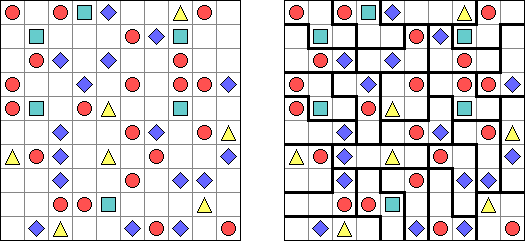
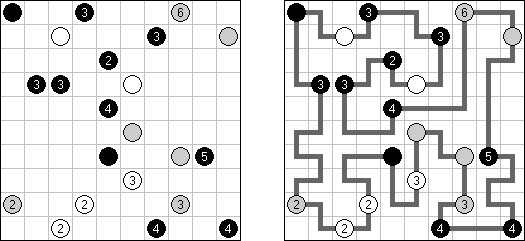
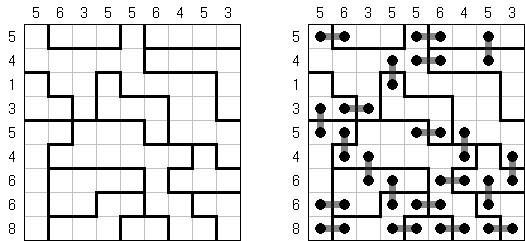
Link-a-Pix ("Paint by Pairs")是一种数字谜题。在格网里除了1数字以外都有重复的数字。需要将成对的数字用一条线连接起来,并且该条线通过的方格数量要相当于该条线起点和终点的数字。连接的线可以是曲线,并将数字水平或垂直地连接起来(但是对角线方向不允许),而且折线不得交叉或经过同一个方格。
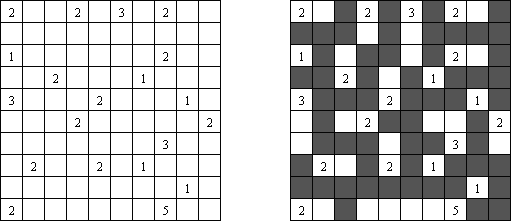
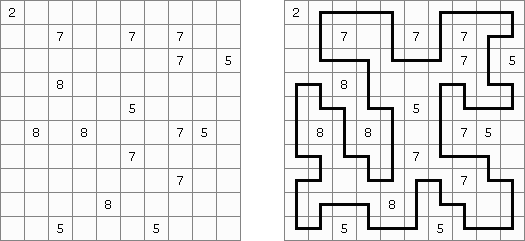
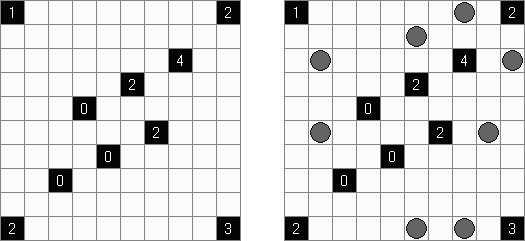
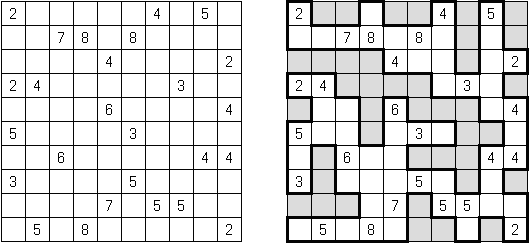
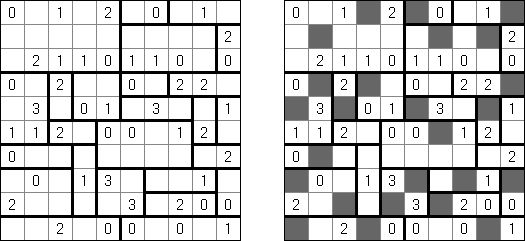
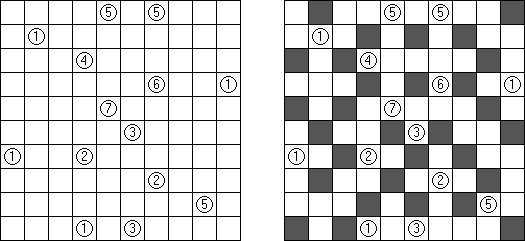
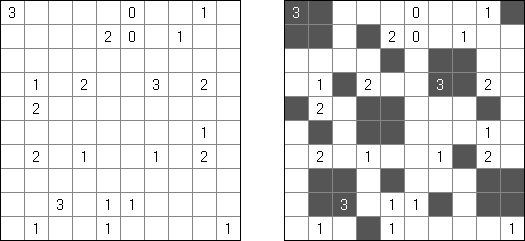
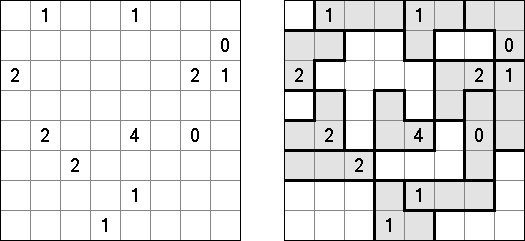
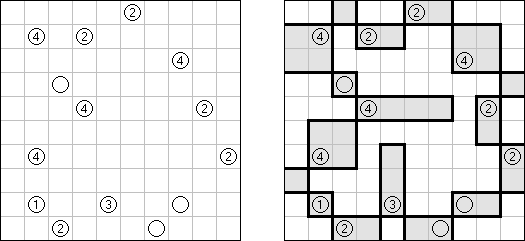
Fill-a-Pix ("Mosaic", "Magipic", "Nurie Puzzle", "Fill-In") 是一种用数字拼图的逻辑谜题。每个数字指出要涂黑多少邻接的方格(包括该数字的方格),比如,如果在方格中有"0"数字,那这个方格及其邻接的方格都不需要涂黑。
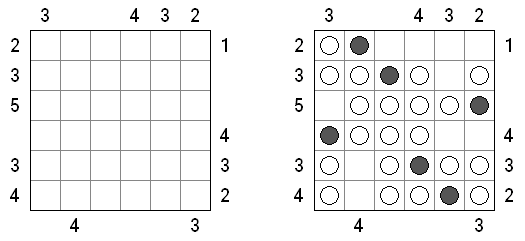
Battleships (战舰游戏,"Solitaire Battleships", "Battleship Solitaire") 是一种谜题,其规则和一款有名的游戏相似。需要在盘面上摆放"船舰",主要条件是"船舰"在对角和邻边都不可以相邻。右边和下面的数字表示在相应的行或列里有几个"船舰"的部分。
Battleships标准盘面是10×10。在例子中有一个占据4个方格的"船舰",两个占据3个方格的"船舰",三分占据2个方格的"船舰"和四个占据1个方格的"船舰"。有时"船舰"有的部分已知。
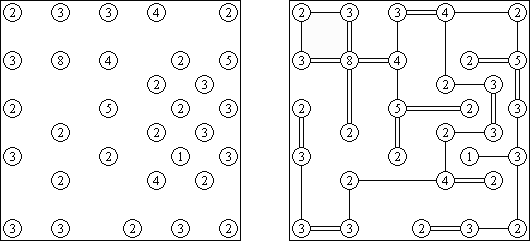
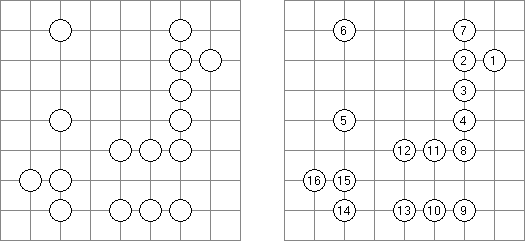
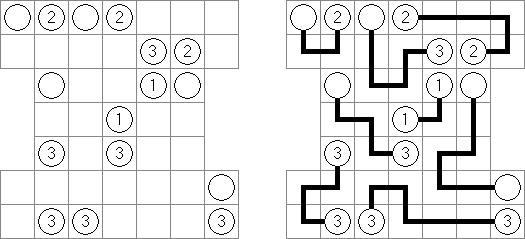
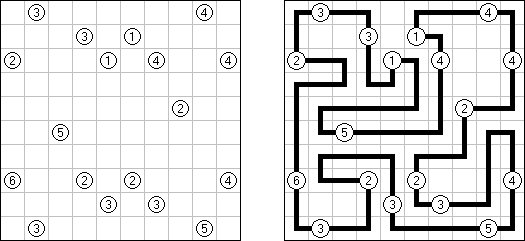
Hashiwokakero ("桥梁"或"筷子","Hashi", "Bridges", "Chopsticks", "Ai-Ki-Ai") 是一种谜题,需要将包含数字的圆圈(孤岛)用直线("桥梁")连接起来。每座岛的数字表示要架到该岛的桥梁的数量;所有的岛要彼此相通,可以从一座岛通过桥梁达到任何岛。 两座岛中间的桥梁数量不得多余2座,可以水平或垂直地划条线(对角线方向不允许),条线不得对折起来或相交叉或贯穿岛。
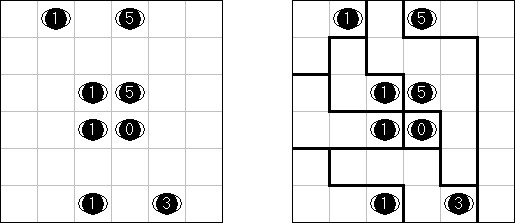
Masyu ("Shiroshinju Kuroshinju", "White Pearls and Black Pearls") 是一种逻辑谜题,需要将白色和黑色的圆圈用横线和竖线连接起来以构成一条不交叉的回路。这条线要直接通过白圆圈,并在前一个或后一个方格中(或在这两个方格中)改变方向。这条线通过黑圆圈时,要在包含黑圆圈的方格里改变方向,在前一个或后一个方格中不得折起来。
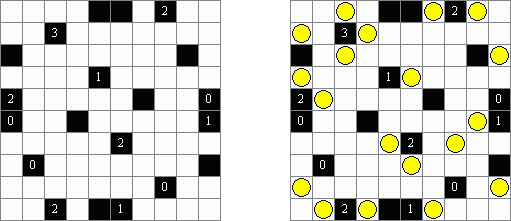
Light Up (点灯,"Akari", "Bijutsukan") 是一种逻辑谜题。盘面分为白色方格和黑色方格,其中有的黑色方格包含数字。需要将"灯"摆放在白色方格中,以"照亮"全盘面,但"灯"不得相互"照亮"。 "灯"可以横向或纵向地发光,但也可以由黑色方格折断。在黑色方格中可以有一个0至4的数字,其表示该方格周围有多少"灯"(不包括在该黑色方格的斜对方向上摆放的"灯")。如果方格不包含数字,那在其周围上可以摆放的"灯"数量不限。
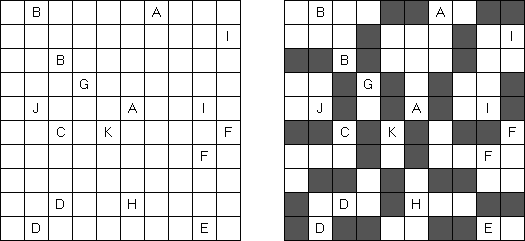
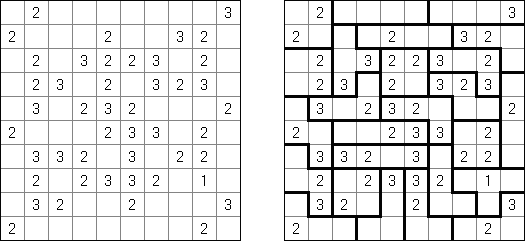
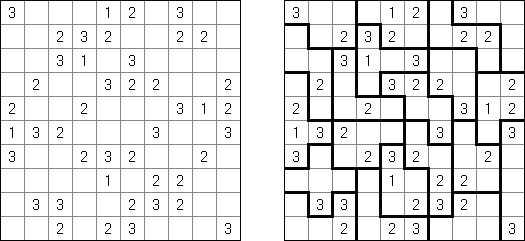
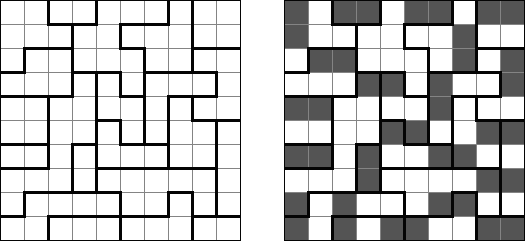
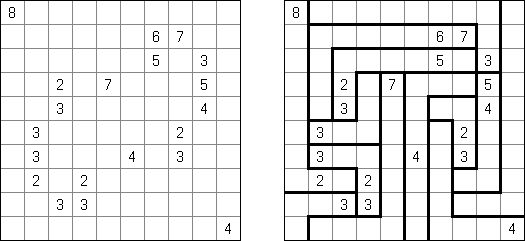
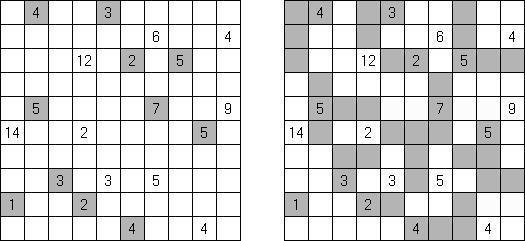
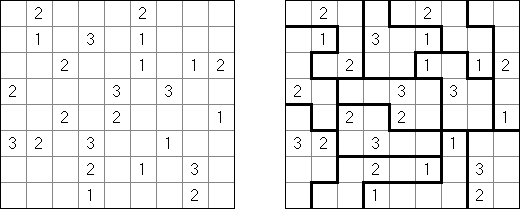
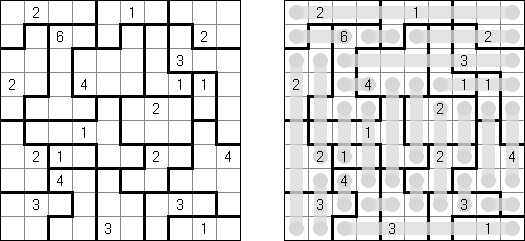
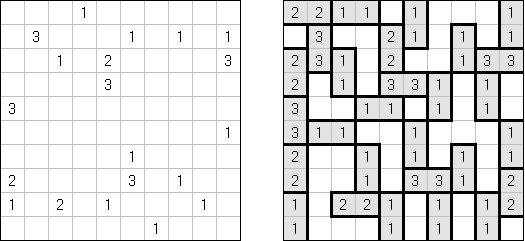
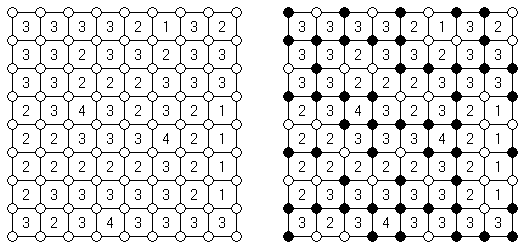
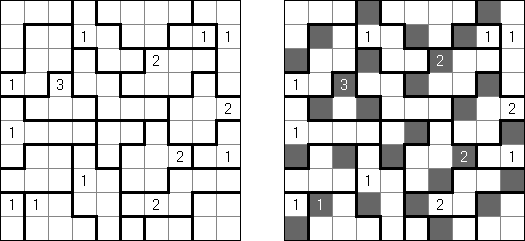
Fillomino ("Polyominous")谜题的盘面是大小随意的长方形格网,在有的小格中有数字。需要将盘面分为几个大块,每个大块包含的小格数量要相当于大块的小格包含的数字。大小相同的大块不可以水平或垂直地相连。不包含数字的小格也可以构成大块,有助于解决该谜题。
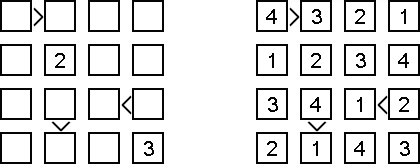
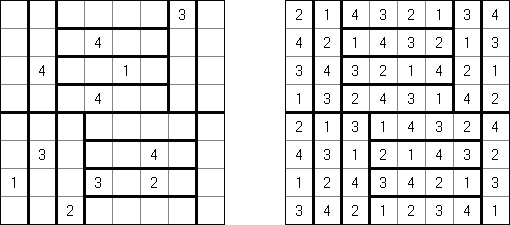
Futoshiki ("不等式","Hutoshiki", "Unequal") 是一种数字谜题。盘面是正方形格网,在有的小格中有数字;小格中间可以有"<" 和 ">"符号,这两种符号表示邻接的数字大小对比。需要将数字填入空方格中,并且数字在每行及列里不能重复。
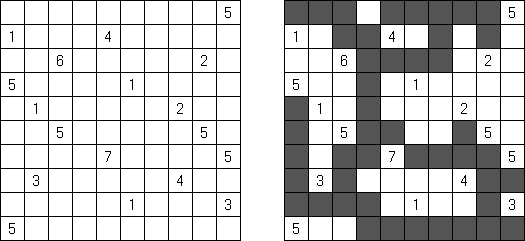
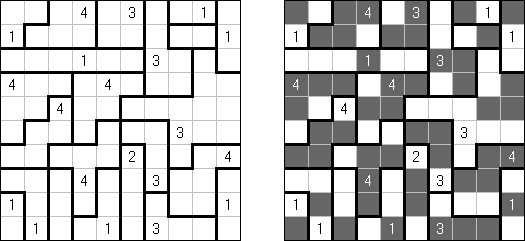
Kuromasu ("Kurodoko", "Where is Black Cells?") 谜题的盘面是长方形格网,有的方格包含数字。需要按照以下条件将方格涂黑:
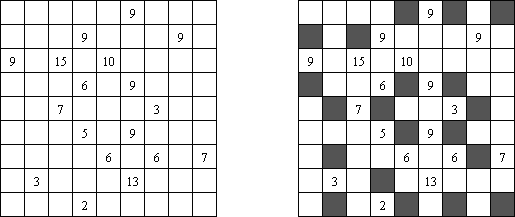
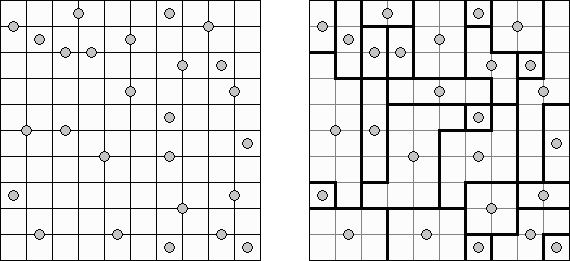
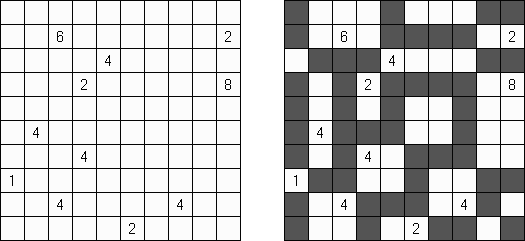
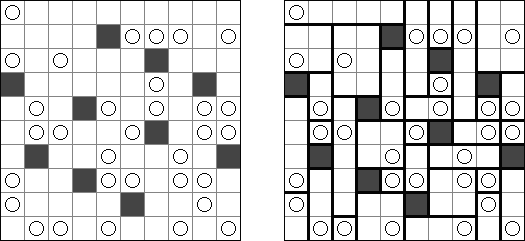
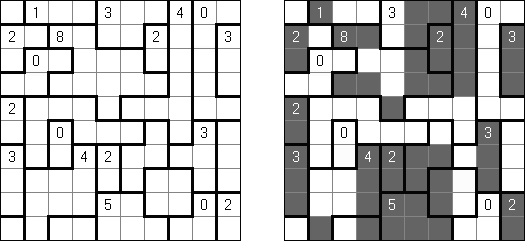
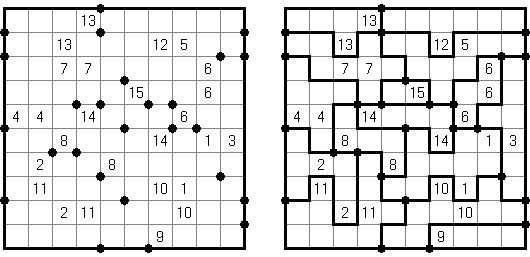
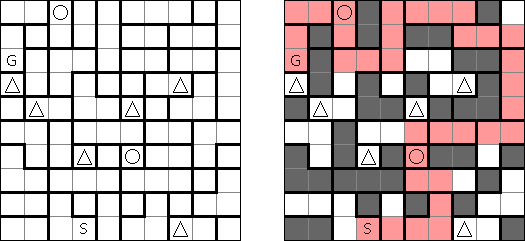
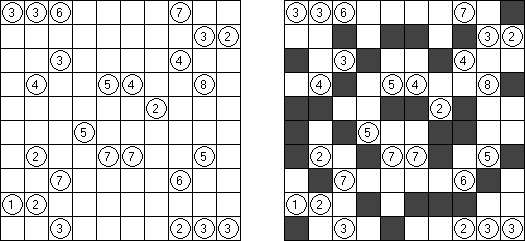
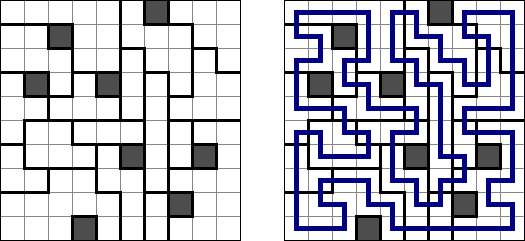
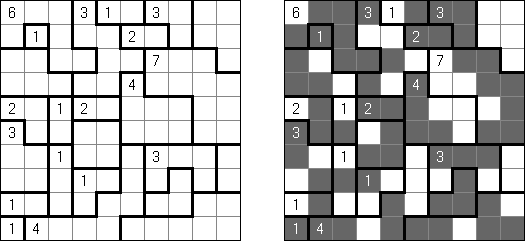
Nurikabe (数墙或"神奇笔刷","Cell Structure", "Islands in the Stream") 是一种数字谜题。在日本神话中,"Nurikabe"是一面隐形的墙,它会阻档旅人的路,使人迷失方向。 需要按照以下规则恢复岛位置的地图:
Sashikabe combines Nurikabe puzzle with Sashigane puzzle. The goal is to blacken some cells of a grid according to the following rules:
Yajikabe was invented by Naoki Inaba (Japan): he combined Yajilin and Nurikabe puzzles. The goal is to blacken some cells of a grid according to the following rules:
Tents ("搭帐篷","Tents and Trees")谜题的盘面是长方形格网,有的方格包含"树"。需要按照以下规则在"树"周围上搭帐篷:
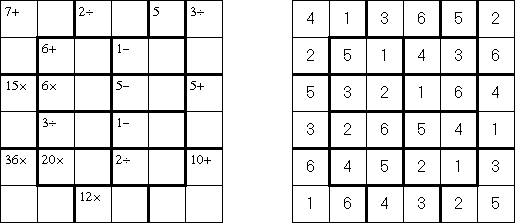
Calcudoku (贤贤, "KenKen", "KENKEN", "KenDoku", "Square Wisdom") 是一种数学逻辑谜题。需要将数字填入格网,在每行和每列里不能重复。每个粗线条围成的区域上角的数字是该区域里的数字算术的结果。与Killer Sudoku相比,这种谜题中在区域里的数字可以重复。
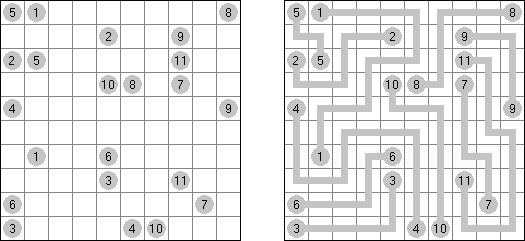
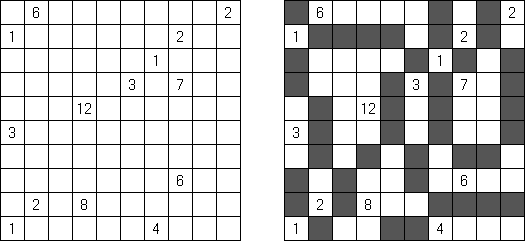
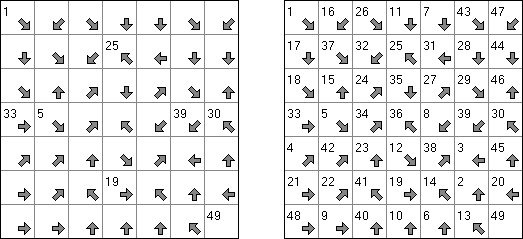
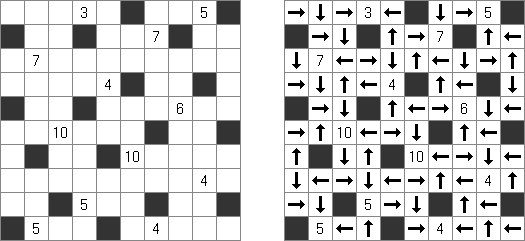
Hidato (意第绪语:"我的谜题")谜题由以色列数学家Gyora Benedek制作。Hidato的盘面是随意形式的格网(一般是长方形或正方形)。目的是水平或垂直或斜对地填上连续的数字。在格网中有已知的最小数和最大数。另外,在盘面上还会给出其它的数字,来降低谜面的难度,并且保证谜面只有唯一的解法。
Numbrix是一种逻辑谜题。在长方形格网中有已知的数字,需要将连续的数字水平和垂直地填入空的方格,对角的方向不准填入。
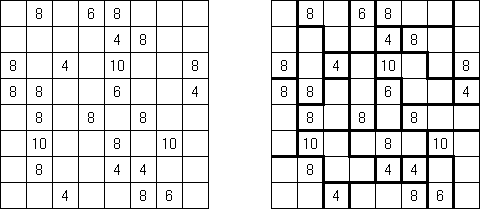
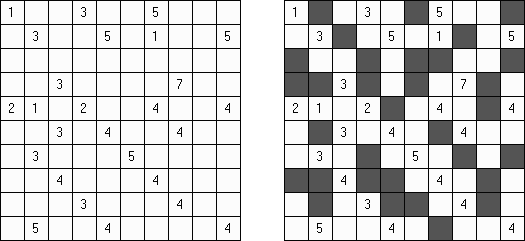
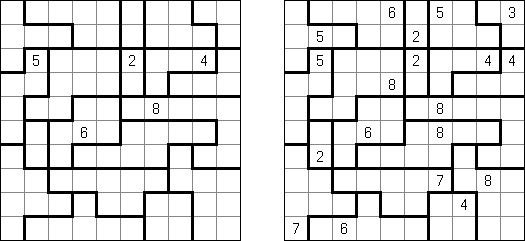
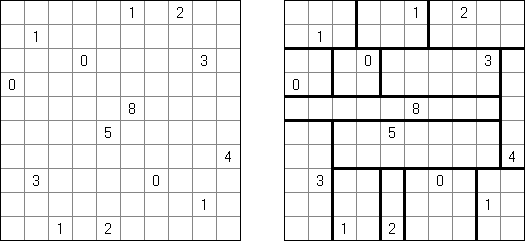
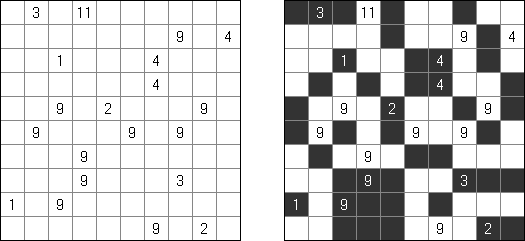
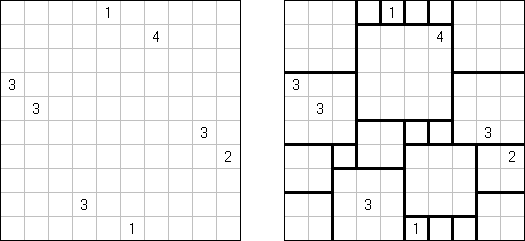
Shikaku (数方或"方形的切口","Divide by Squares","Divide by Box", "Number Area") 是一种逻辑谜题。其盘面是随意大小的长方形格网,有的方格包含已知的数字。规则是:需要划出粗的线使全格网分为长方形或正方形的"区域",每个"区域"要包含一个数字,数字要等于该"区域"占据方格的数量。
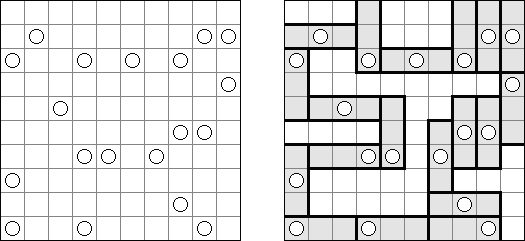
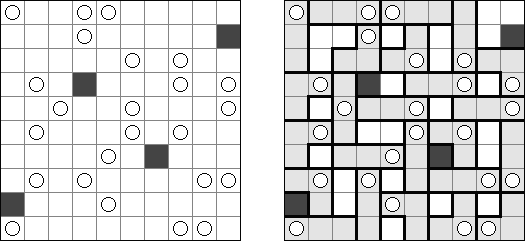
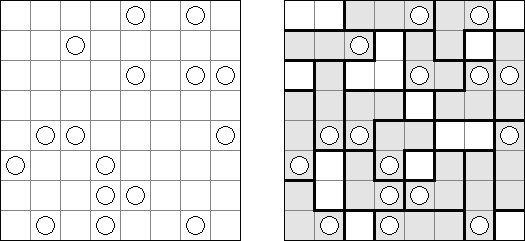
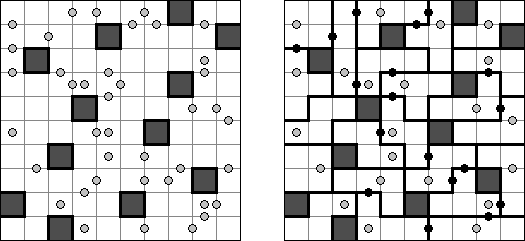
Galaxies ("星系","Tentai Show") 是一种涉及逻辑学和几何学的谜题。需要将包含圆圈的长方形格网分为"区域";每个"区域"只能包含一个圆圈,而且圆圈要处在"区域"的对称中心。
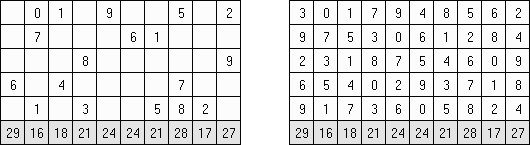
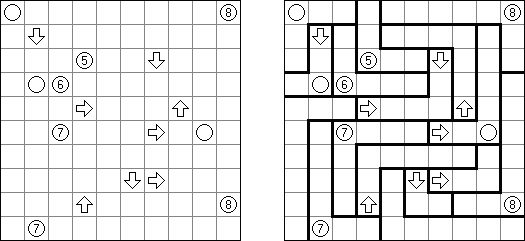
Skyscrapers ("摩天楼")是一种逻辑谜题。目标是在格网中填上数字,数字在每行和每列里不得重复。要填上的数字表示在方格中的楼有多少层;格网对外的数字指出能看到几个在相应的行或列里的楼(比如,由于六层楼,无法看到下一个四层楼)。
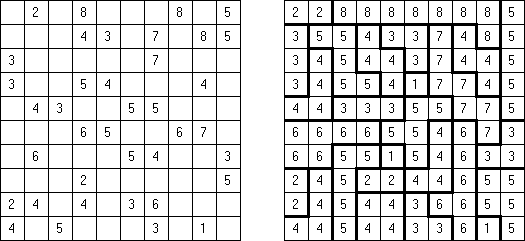
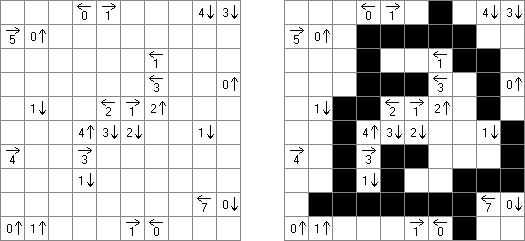
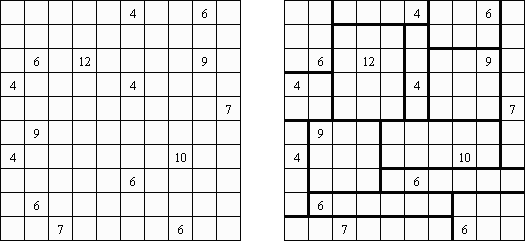
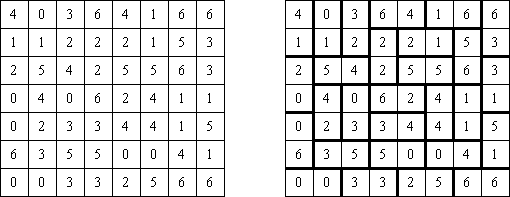
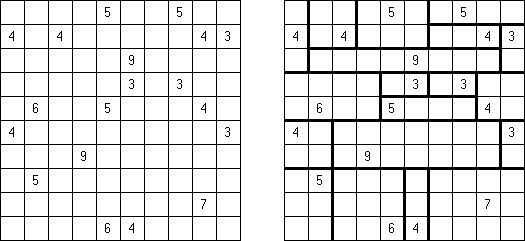
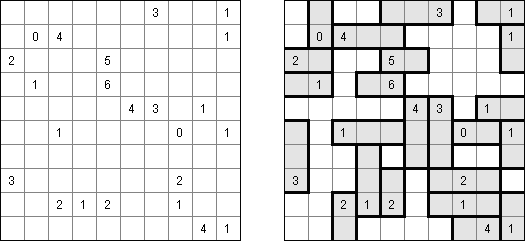
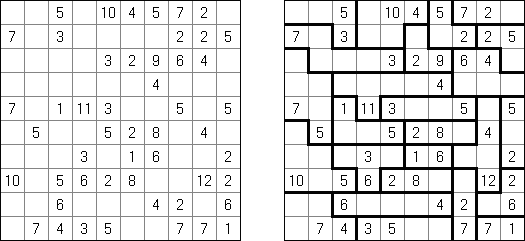
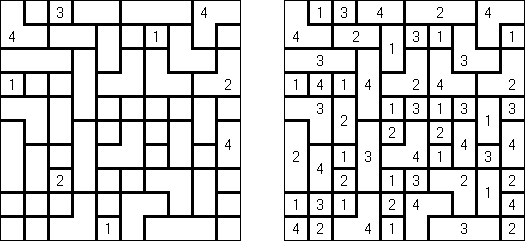
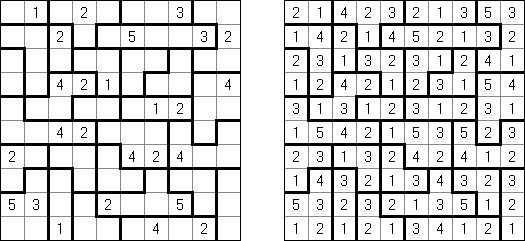
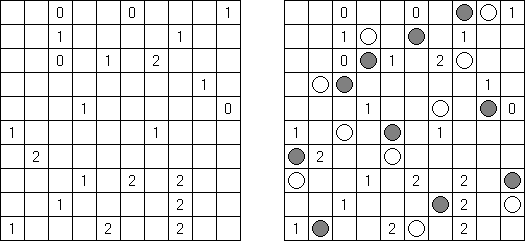
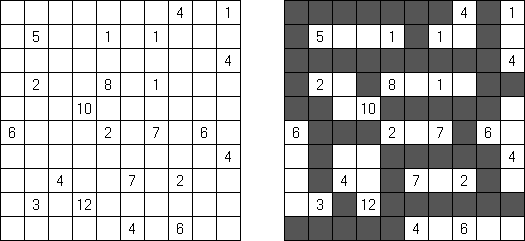
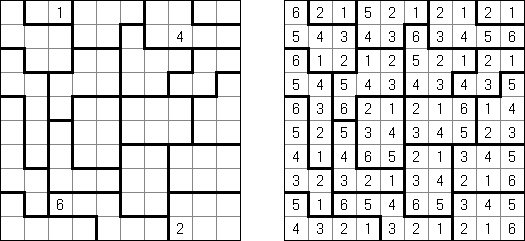
Hakyuu ("波纹作用","Ripple Effect", "Seismic") 是一种逻辑谜题。长方形格网分为大块("房间"),在有的小格中有数字。需要在所有的小格中填上数字使每个大块都包含1到与该大块所占据的方格数量相等的数字。如果在某行或列里有两个重复的数字,那重复的数字之间的小格数量要等于或大于该数字。比如,一列里有两个包含"5"数字的小格,它们之间的小格数量要等于或大于5。
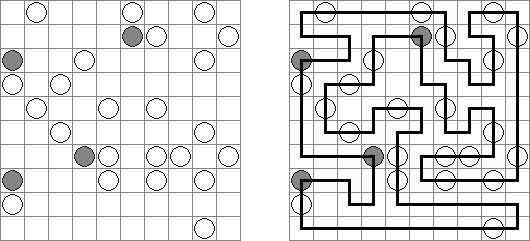
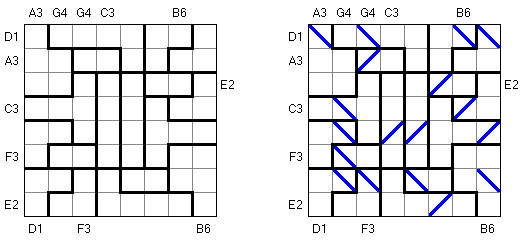
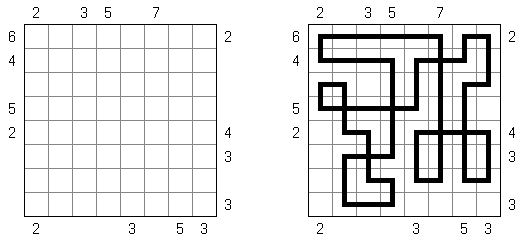
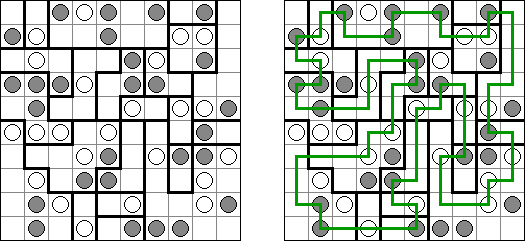
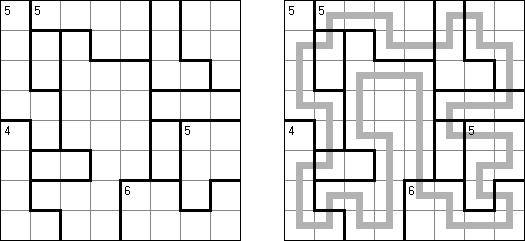
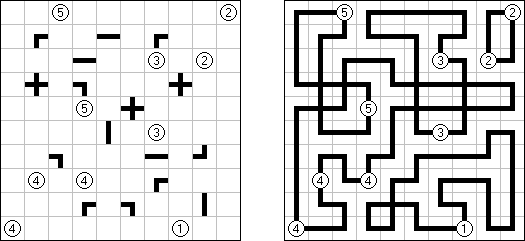
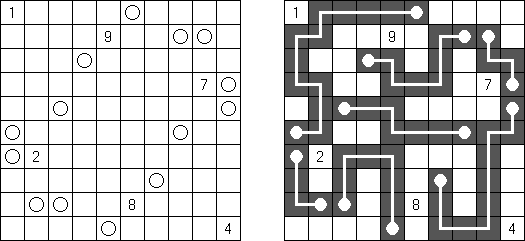
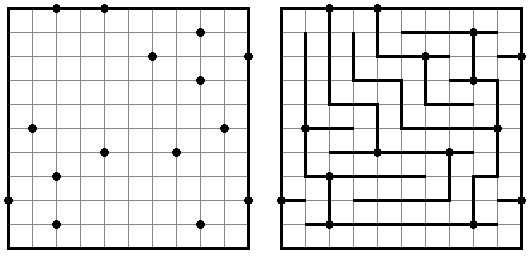
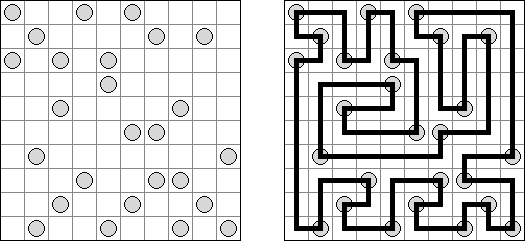
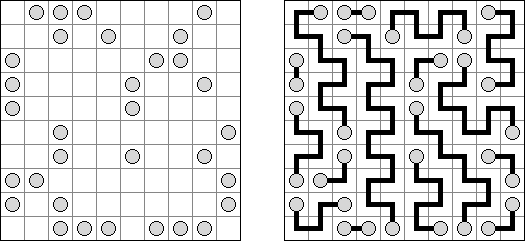
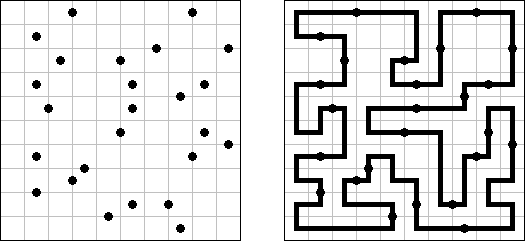
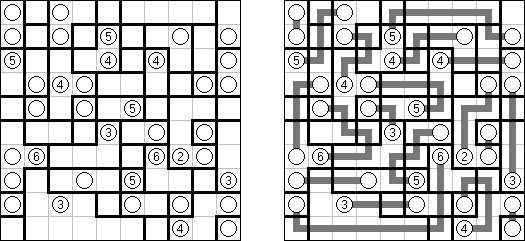
Grand Tour ("伟大的旅行") 是一种逻辑谜题。需要在长方形或正方形格网中将所有的圆点用一条不交叉的回路连接起来。为了保证谜面的解法的唯一性,有的圆点已用线段连接。
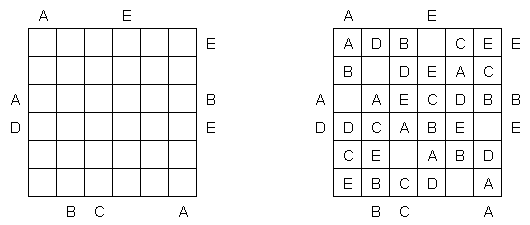
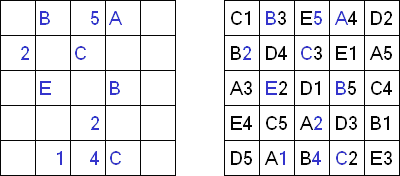
Easy as ABC ("跟"ABC"一样简单","ABC End View", "Last Man Standing")是一种包含字母的逻辑谜题。需要在正方形方格中填上拉丁字母(比如,A至E),每个字母在每行或每列里不能重复。在方格中可以留空的小格;方格外的字母表明将该字母要摆放在相应的行或列的第一个方格中。
Clouds ("云","Radar")是Battleships谜题的种类。需要在随意形式的格网中将方格涂黑块("云"),"云"在相邻或者对角方向不得相连。方格右边和下面的数字指出"云"占据的方格数量;"云"的数量和大小未知,已知的是"云"侧面占据的方格数量等于或大于2个。
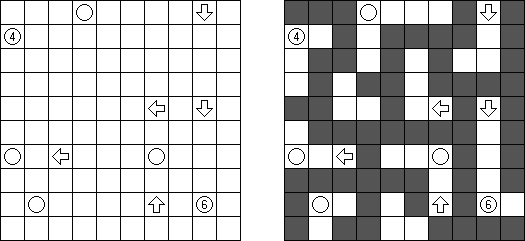
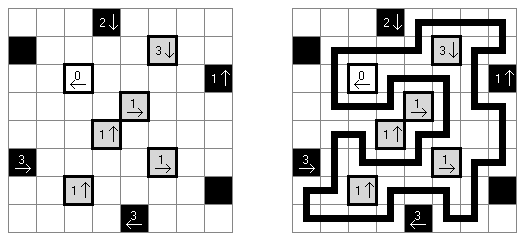
Yajilin ("箭头圆环","Arrow Ring","Straight and Arrow") 是一种逻辑谜题。在正方形或长方形格网中有数字和箭头符号,它们指出黑色方格在格网中的位置。谜题的目标是画一条不交叉而不通过包含箭头的方格或黑色方格的回路。 The grid may contain gray cells that can not be part of the loop.
Minesweeper (扫雷)是一种Microsoft Windows操作系统用户都知的游戏。需要按照数字在空的方格中布雷。每个数字指出了附近区域中地雷的数量。一个方格能包含一个地雷,在包含数字的方格中不布雷。
Minesweeper Battleships ("扫雷战舰", "Battlemines")结合了两款流行的谜题游戏。需要在盘面上摆放"船舰", "船舰"在对角都不可以相邻。方格的数字表明在该方格周围(包括对角)有几个"船舰"。
Heyawake (数间)是一种逻辑谜题。长方形格网分为大块("房间"),其中有的大块包含数字;数字指出该大块要占据的黑色方格数量。如果在大块中没有数字,该大块占据的黑色方格数量不限。
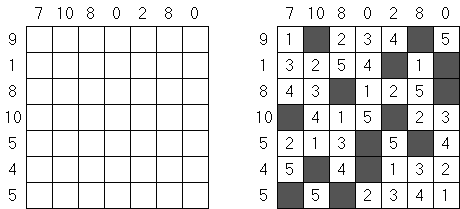
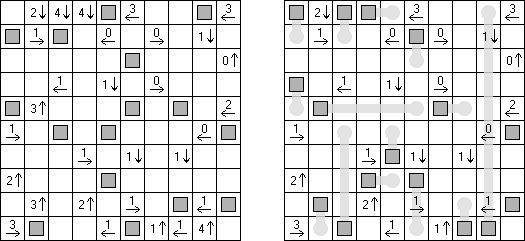
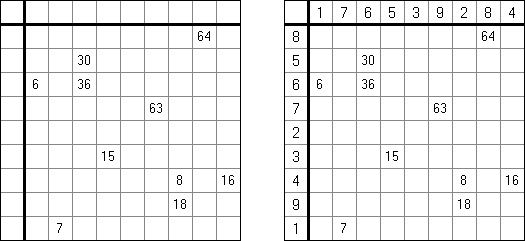
Tenner Grid ("From 1 to 10", "Zehnergitter", "Grid Ten") 谜面是宽度等于10个方格的长方形格网。需要填入格网使每行包含1至9的数字,在列里数字可以重复。格网下面的数字表明该列里面所有数字之和。在横向相邻的方格中(包括对角方向的方格)数字不得重复。
Hundred ("一百")谜题中,正方形格网的每个小格都有数字,需要加上数字使每行和列里的数字之和等于一百。
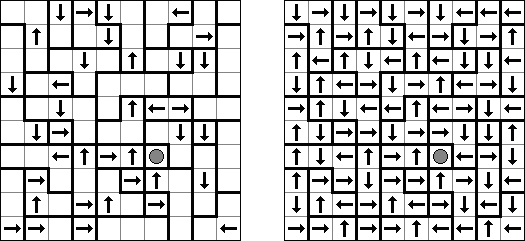
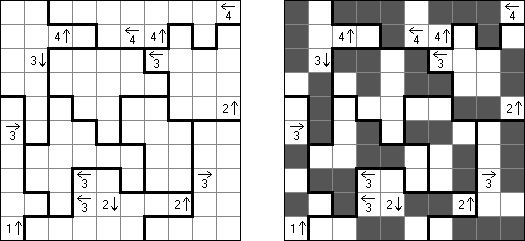
Arrows ("箭头")是一种逻辑谜题。长方形或正方形的格网有数字。谜题的目标是在格网外面摆放箭头;每个箭头最少要指示一个包含数字的方格,数字表示指向该方格的箭头数量。
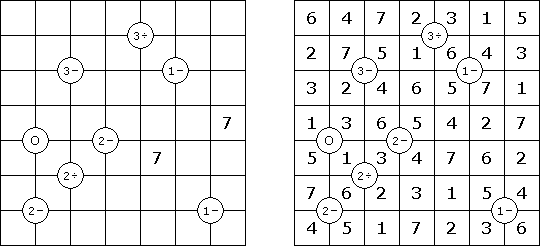
Mathrax也是一种逻辑谜题。需要在正方形的格网中填上数字,在每行和每列里不重复。有的方格有已知的数字,而且格网中也可能有表示下面条件的圆圈:
Str8ts (顺独,"Straights"是扑克术语)是一加拿大人Jeff Widderich制作的种逻辑谜题。正方形的格网分为黑色和白色的方格,需要在白色方格中填上连续数字,数字不需要按从大到小的顺序排列(比如,2-1-3-4)。在白色方格和黑色方格中的数字在每行或每列里不得重复。连续数字组不包括黑色方格的数字。
Linesweeper是一种逻辑谜题,其规则和扫雷谜题相似。在正方形或长方形的格网中有的方格有数字(0至8)。需要划一条通过方格的不交叉的回路,它不得通过包含数字的方格。数字指出那条线通过该数字周围的方格的数量。
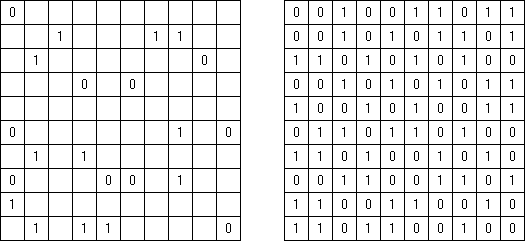
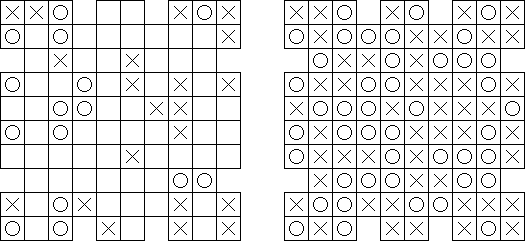
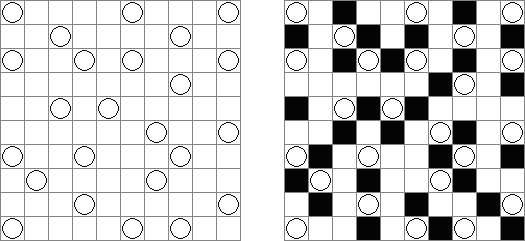
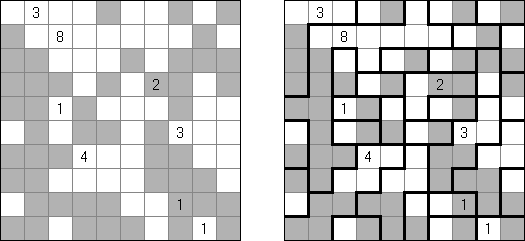
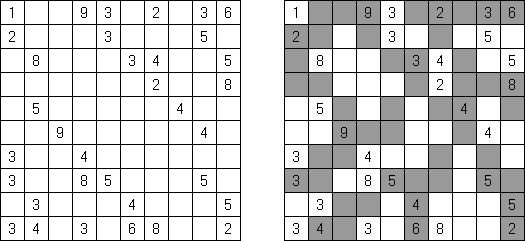
Binairo (二元的谜题,"Binary Puzzle","Takuzu","Tohu wa Vohu") 是一种使用"0"和"1"数字的逻辑谜题。需要按照以下规则将数字填入长方形或正方形的格网中:
Walls ("墙")是一种逻辑谜题,是由日本人Naoki Inaba发明的。需要在白色方格中划出水平线和垂直线使从黑色方格中发出的线总长度与黑色方格中的数字相符。
Dominosa ("数邻","Dominosa Omnibus","Solitaire Dominoes","Domino Hunt")是一种使用多米诺骨牌的逻辑谜题。在盘面上只有数字;需要"恢复"骨牌之间的界线。
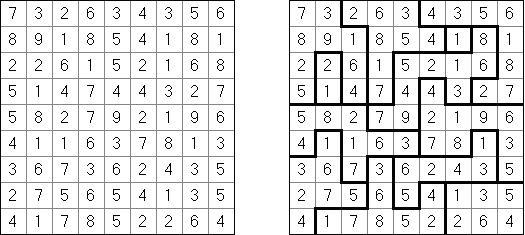
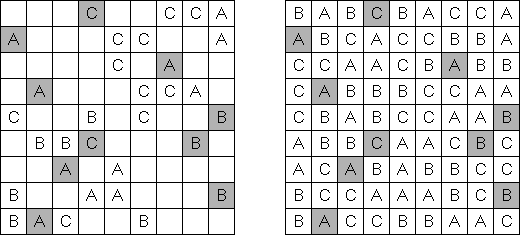
Patchwork ("帕奇维克","Tatami")是一种将格网分为同样尺寸的地区("房间")的谜题。需要在每个房间摆放数字,数字要等于从1至该房间包含的方格数量。每列和每排要包含每个数字的同样数量。水平或垂直相邻方格的数字不得重复。 这种谜题还可以使用字母代替数字。字母和数字的谜题Cross+A软件都能解答。
Knossos ("克诺索斯"是克里特岛上的古城和王宫,也作为米诺陶洛斯被关进的迷宫所在地)是一种谜题,在长方形或正方形格网里的几个方格有数字。需要将格网分为地区("房间")使每个地区只有一个数字。这个数字要相当于该"地区"周长。
Rekuto是正方形或长方形格网的逻辑谜题。有的方格有数字。需要划出将格网分为长方形和方形地区的粗线使每个地区只包含一个数字,这个数字要等于该地区的宽度和高度的总和。
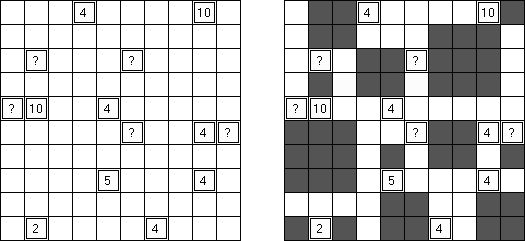
Neighbours ("邻居")是一种任意形状格网的逻辑谜题。有的方格包含数字或问号。需要将格网分为地区,每个地区的方格数量相等。每个地区只可以有一个包含数字(问号)的方格;这个数字表明该地区有几个"邻居"。如果两个地区有共同的界线,那算是邻居。如果地区有包含问号的方格,该地区的"邻居"数量不限。
Four Winds ("四风","Line Game")是一种逻辑谜题,正方形或长方形的格网有黑色和白色的方格。需要划出直线,那些直线要从黑色方格出发并经过所有白色方格。在黑色方格中的数字表明那些直线占据几个白色方格。直线不得交叉。
Shakashaka("摇一摇","Proof of Quilt")是一种逻辑谜题,正方形或长方形的格网有白色和黑色的方格;其中黑色方格有数字(0至4)。需要在白色方格中摆放黑色三角形以形成白色的长方形和正方形。有的白色方格可以留空。那些地区可以有水平、垂直或斜对的位置。邻近的白色地区不得有共同的面。黑色方格的数字表明有几个三角形与该方格接邻。
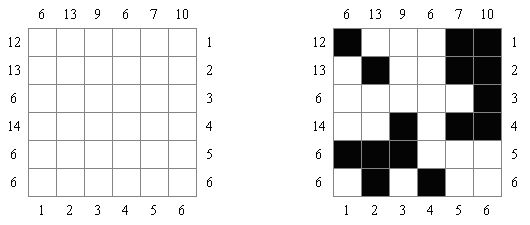
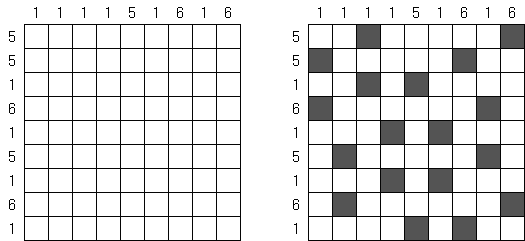
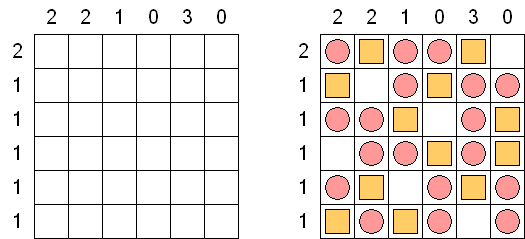
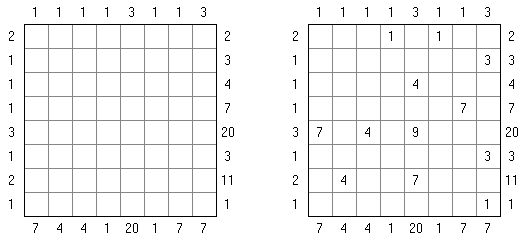
Kakurasu ("Index Sums") 是一种逻辑谜题,需要在正方形或长方形的格网中划出白色和黑色的方格。处在格网左边及上面的数字表明在行和列中的黑色方格"重量"之和。处在格网右边及下面的数字指明在相应的行和列中的黑色方格的"重量"(第一行和第一列的黑色方格的"重量"等于1,第二行和第二列的黑色方格的"重量"等于2, 等等)。
Mochikoro ("Mochinuri") 逻辑谜题使用长方形或正方形的格网,几个方格有数字。需要通过划出白色方格和黑色方格的方式形成白色方格构成的长方形或正方形的"岛"。
Seethrough ("看透","Doors","Open Office") 是一种逻辑谜题,正方形或长方形的格网中的每个方格表明"房间"。需要关或开房间之间的"门"。打开的门让从一个房间看到另一个房间或看透几个房间。在方格中的数字表明从这个房间能看到的房间数量(不算该房间)。在格网中的部分都不得单独,从任何房间能到任何房间。
Lighthouses ("灯塔")是一种逻辑谜题,在格网中有包含数字的黑色方格("灯塔")。数字表明该灯塔照亮的船舶数量。灯塔照亮的船舶处在该灯塔的行或列中,在灯塔和船舶之间可以有其他船舶及灯塔。每个船舶由至少一个灯塔照亮。船舶不得接触到任何灯塔或其他船舶,在对角也不得接触。
Lighthouse Battleships:
Tapa 逻辑谜题,是由土耳其人Serkan Yurekli发明的。这种谜题使用正方形或长方形的白色格网。需要遵守以下条件用黑色涂上方格:
Fobidoshi ("Forbidden Four") 是一种由日本人Naoki Inaba发明的逻辑谜题。使用长方形或正方形的格网,几个方格有小圆圈。需要将小圆圈放在空的方格中,小圆圈要在水平或垂直的方向相互接触。水平或垂直地接触的小圆圈数量不得超于4个。
Island ("岛","Tents Island","Airando")是一种逻辑谜题,是由日本人Naoki Inaba 发明的。这种谜题使用格网,有的方格包含数字。需要涂黑方格,以白色的方格形成同一的岛。有数字的方格是岛的部分。数字表明在岛上从该数字的方格能水平或垂直地达到的不包含数字的白色方格数量(以包含数字的其他方格为界限)。
Dominion谜题使用格网,有的方格包含字母。需要按以下规则将方格涂上黑色:
Tren是一种谜题,是由日本人Shinichi Aoki发明的。这种谜题的名称从日语翻译成“停车处” (每一个区块是“汽车”, 全格网是停车处)。这种谜题使用正方形或长方形的格网,有的方格包含数字。需要将格网分为1x2 或1x3的区块。每个数字要在一个区块里面。数字表明,可以将区块移动几个方格。区块只向短边的方向移动。
No Four in a Row ("在一行中没有四")迷题使用自由形的格网。几个方格有“〇”和 “× ”符号。需要用这些符号添上其他方格,在水平、垂直或对角线的方向不得一连摆放三个以上相同的符号。
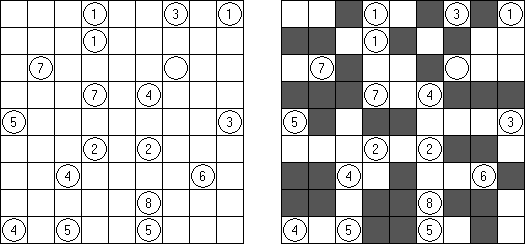
Corral ("Bag","Cave")是一种使用长方形或正方形格网的谜题,几个方格有数字。需要在所有的数字周围画出闭合的线。数字表明在闭合的线内从该数字的方格能水平或垂直地看到的方格数量,包括该方格。
Foseruzu ("Four Cells")是一种逻辑迷题,主要使用正方形或长方形的格网,里面有数字。需要将格网分为包含4个方格的大块。数字指出该方格的几个侧面形成大块的界线(格网的外部线也算为方格的侧面)。
Faibuseruzu ("Five Cells","Solomon's Keep"):此迷题的条件和Foseruzu一样,区别是格网分为的大块包含5个方格。
Sutoreto ("Sutoretokurosu" 是英文名称“Stright Cross”的日本发音) 是日本人Naoki Inaba 为发明家的逻辑迷题,使用长方形或正方形的格网,里面有白色和黑色的方格。一些白色方格有数字。需要在其他白色的方格中摆放数字以在黑色方格中间形成横向和纵向的数组,这些数组由连续的数字组成(不一定按顺序摆放数字,例如,2-3-4 或5-4-7-6)。
Renban迷题使用正方形的格网,格网分为自由形的大块。需要用数字填满格网,数字在任何行或列或大块里不得重复。在一个大块内的数字都是一排连续的数字(但不一定按顺序摆放的,例如,5-3-4)。
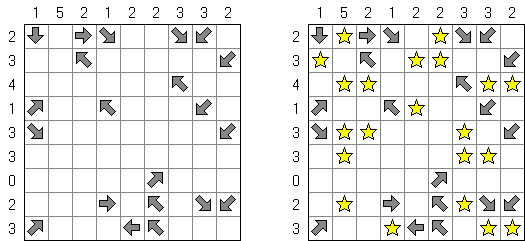
Buraitoraito (英文名称“Bright Light”的日本发音)是日本人Naoki Inaba为发明家的逻辑迷题。 此迷题使用正方形或长方形的格网,里面有白色和黑色的方格。需要在白色的方格中摆放星星;在黑色方格中的数字指出在水平和垂直的方向有几个星星(此黑色的方格为起点,格网界线或其他黑色方格为终点)。
Irasuto (“插画”,"Illustration")是一种逻辑迷题,由日本人Naoki Inaba 发明的。此迷题使用长方形或正方形的格网,里面有白色和黑色的方格。其中几个方格包含数字。需要按以下条件涂黑方格:
Suguru ("Number Blocks") 是一种逻辑迷题,由日本人Naoki Inaba发明的。此迷题使用正方形或长方形的格网,格网分为几个大块。需要用数字填满格网以任何大块包括1至该大块里面的方格数量的数字。包含相同数字的方格不得水平、垂直或对角线地毗邻。
Trinudo逻辑迷题使用正方形或长方形的格网。几个方格有数字。需要将格网分为由一个、两个或三个方格构成的大块。同样的大块在横向和纵向都不得相连。数字指出此数字属于的大块包含几个方格。
Creek ("Kuriku") – 是一种逻辑益智游戏, 也是正方形或长方形的网格; 包含从0到4的数目的圈儿可以放置在该线的交叉点。数目是指相邻的黑色方格的数量。必要将黑色和白色的方格摆,使所有的白色方格彼此接触,垂直或水平。
Gappy – 是一种逻辑益智游戏,这是一个正方形网格。必要将黑色正方形网格中,使得每行和每列有两个黑的方格。两个黑色的方格别相接触(连它们的角也都不能相接触)。网格外边数目代表行或列的黑色方格中间的白色方格数目。
Norinori – 是一种逻辑益智游戏。它区为长方形或正方形网格分成任意形状的宫格。在每个宫格必要黑漫两个方格。每个宫格必要黑漫两个方格。黑漫方格必须形成2×1或1×2(骨牌)组,不分区域限度。两个黑色的方格别相接触(但是它们的角能相接触)。
Yonmasu ("Yonmasubunkatsu") – 自日本来的逻辑益智游戏是被直树稻叶(Naoki Inaba)想出的。它的目的是矩形或正方形形状的网格。有些方格含有小圆圏。网格必须被划分成多个区域,一个4方格,使得每个区域包含一个小圆圏。
Bricks – 是一种逻辑益智游戏。需要填写的网格数字,使它们在每一行和每一列都不会重复。在每块砖一幅数字是偶数,其他数字 - 奇数。
Number Chain (数字链) - 是一种被俄罗斯列奥尼德Mochalov 发明的数字迷题 (Leonid Mochalov)。任务是一个长方形或正方形网格,每个网眼包含一个数字。在网格的左上角是数字1,在右下角 - N; 剩下的网格单元包含任意数量从1到N。 必要的是铺平道路从网格的左上角至右下角,使曲折线通过不反复的数字的N方格。
Kapetto ("Settokapetto", "Set Carpets") - 是一种被日本人的直树稻叶逻(Naoki Inaba)想出的辑益智游戏。是一种谜题,在长方形或正方形格网里的几个方格有数字。必要将长方形的方格摆,使每个地区只有一个数字。这个数字要相当于该"地区"周长。正方形的格网可能包括任何地区不属于的方格。
Renkatsu - 是一种被日本人的直树稻叶逻(Naoki Inaba)想出的辑益智游戏。在正方形或长方形格网中有数字。需要将格网分为地区使每个地区只有一个数字从1到N。N是地区的大小。
Eulero (希腊拉丁方阵, "Graeco-Latin Square", "Euler Square") - 是一种字母数字迷题。您必须填写符号正方形网格,以便在满足下列条件:
Anraikumozaiku ("Unlike Mosaic") - 是一种被日本人的直树稻叶逻(Naoki Inaba)想出的辑益智游戏。任务为矩形或正方形形状的网格。有些方格含有小圆圏。网格必须被划分成多个区域,一个4方格,使得每个区域包含一个杯子。网格必须被划分成矩形形状的区域,使得每个区域包含一个杯子。黑色单元不属于任何区域。含有方格相同数量的区域垂直或水平都不可以相邻。
Kurotto - 一种逻辑谜题。任务是矩形或正方形网格,一些方格含有方格(空白或数字)。要放置黑白方格在下列条件下:
Tasukuea - 一种逻辑谜题。它的目的是矩形或正方形网格,一些方格含有数字或问号。要放置黑白方格在下列条件下:
Star Battle consists of a square grid divided into regions. The goal is to place stars into some cells in the grid so that each row, column, and region contains the same number of stars. Stars cannot be placed in adjacent cells, not even diagonally.
Araf (from Turkish, literally "purgatory"; original Japanese name - "Aidabeya") is a logic puzzle. It is played on a rectangular grid. Some of the cells in the grid are numbered. The goal is to divide the grid into regions such that each region contains exactly two numbers. Each region must have an area that is strictly between those numbers. For example, if the region contains 2 and 5, the region's area must be equal to 3 or 4.
Kabingurodo ("Curving Road") - 是一种被日本人的直树稻叶逻(Naoki Inaba)想出的辑益智游戏。它的目的是矩形或正方形形状的网格。有些细胞含有小圆圏。必要将黑色正方形网格中放置在下列条件下:
Thermometers is a kind of logic puzzles. The grid is filled with thermometers, which are either not filled, partly filled or completely filled. The numbers on the outside indicate how many squares are filled in that row or column. Every thermometer is filled from the base (circular part), towards the top. This does not depend on the actual orientation of the thermometer.
Snake (also known as "Tunnel") is a kind of logic puzzles. It is played on a rectangular or square grid, where two cells are marked. The task is to draw a single line ("snake") between marked cells; this line never touches itself, not even diagonally. Numbers outside the grid show how many cells must be blackened in the corresponding row or column.
Peintoeria ("Paint Area") is a logic puzzle published by Nikoli. The puzzle consists of a rectangular grid of any size divided into regions. The goal is to blacken some cells of a grid according to the following rules:
Irupu ("I-Loop") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains circles in some cells. The goal is to locate some blocks in the grid, having the size either 1 x 3 or 3 x 1. Each block contains one circle and must be orthogonally adjacent to exactly two other blocks. All block cells form one contiguous region.
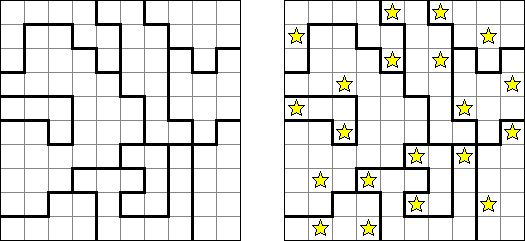
Sashigane (from Japanese, literally "carpenter's square") is a type of logic puzzle published by Nikoli. The goal is to divide the grid into L-shaped regions. The two "legs" of a region must be exactly one cell wide. A circle represents a cell in which an "L" must bend (the grid contains circles not for all regions). A region must have the same number of cells as a number in a circle. An arrow marks the end of the region's "leg"; the arrow points to the cell in which the "L" bends.
Sashikazune is a logic puzzle published by Nikoli. A rectangular or square grid contains numbers in some cells. The aim is to divide the grid into L-shaped regions. The two "legs" of a region must be exactly one cell wide. Each region contains not more than three cells with numbers. The grid may contain regions without numbers. A number indicates the amount of cells up to a place where an "L" must bend (including the cell with the number). A cell with 1 always represents a cell in which an "L" must bend.
Chocona ("Chocolate") consists of a rectangular or square grid divided into regions. The aim is to blacken some cells of a grid according to the following rules:
Different Neighbours consists of a rectangular or square grid divided into regions. The aim is to place a number from 1 to 4 into each region so that no two regions that touch (even diagonally) share the same digit.
LITS ("Nuruomino") is a logic puzzle created by Naoki Inaba (Japan). The puzzle consists of a rectangular grid of any size divided into regions. The goal is to blacken exactly four connected cells in each region, to form an L, I, T, or S tetromino.
The tetrominoes may be rotated or mirrored. When two tetrominoes in adjacent regions share an edge, they must not be of the same type. All tetrominoes must form an orthogonally contiguous area. The tetrominoes must not cover an area of 2 x 2 cells.
Nanbaboru ("Number Ball") consists of a square grid. The goal is to fill in some cells with numbers from the given range. No number may appear twice in any row or column. A cell with a circle must contain a number; a cell with a cross cannot contain a number.
Tairupeinto ("Tile Paint", "Crazy Pavement") consists of a rectangular or square grid divided into regions. The aim is to blacken some cells so that each region is either completely filled or completely empty. External numbers are the clues, and equal the row and column totals for the black squares.
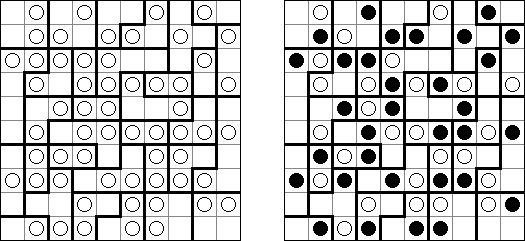
Yin-Yang consists of a rectangular or square grid with white and black circles in some cells. The aim is to place a black or white circle in each empty cell so that all circles of same color are connected to each other, vertically or horizontally. Additionally, no 2 x 2 group of cells can contain circles of the same color.
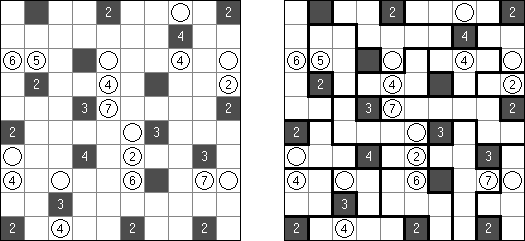
Nanro is a logic puzzle published by Nikoli. The task consists of a rectangular or square grid divided into regions. The goal is to fill in some cells with numbers. All numbers in a region must be the same. The given number in a region denotes how many cells in this region contain a number (all regions must have at least one number). When two numbers are orthogonally adjacent across a region boundary, the numbers must be different. Numbered cells must not cover an area of size 2 x 2 or larger. All cells with numbers must be interconnected.
Light and Shadow is a type of logic puzzles. The aim is to divide the grid into gray and white regions. Every region contains exactly one number. The region must have the same number of cells as the number it contains. Numbers in white cells are part of white regions; numbers in gray cells are part of gray regions. Same colored regions cannot share an edge.
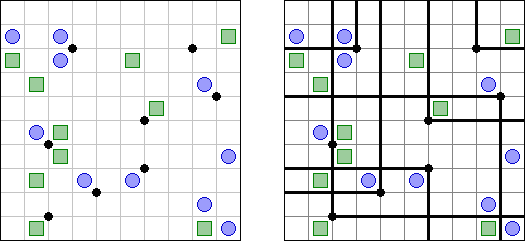
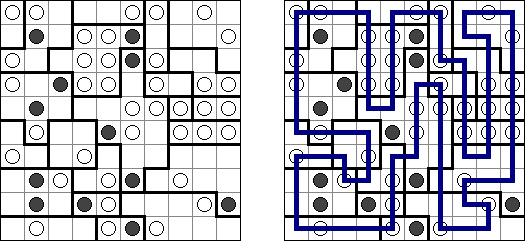
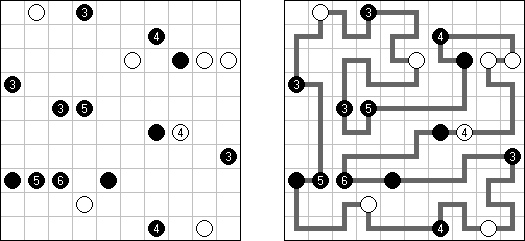
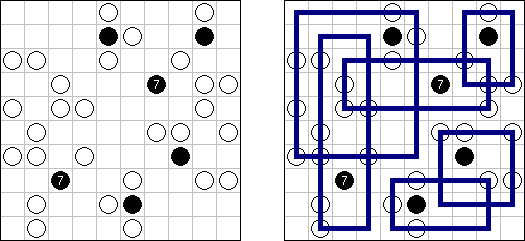
Arukone ("Number Link") consists of a rectangular or square grid with numbers in some cells. The goal is to connect each pair of numbers with single continuous lines. The lines must neither cross nor touch each other.
Tetroid is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains black cells. The aim is to divide the grid into regions of exactly four cells, to form an L, I, T, S or O tetromino.
Black cells do not belong to any tetromino. The tetrominoes may be rotated or mirrored. When two tetrominoes in adjacent regions share an edge, they must not be of the same type.
Sukima (from Japanese "Sukimaburokku"; literally "space between blocks") is a logic puzzle created by Naoki Inaba (Japan). A rectangular or square grid contains circles in some cells. The aim is to locate some regions in the grid, having the size of exactly three cells. Each region contains one circle. Each 2 x 2 area must contain at least one cell, that does not belong to any region. Black cells do not belong to any region.
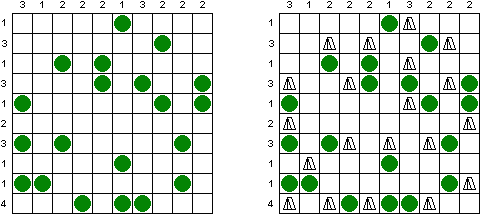
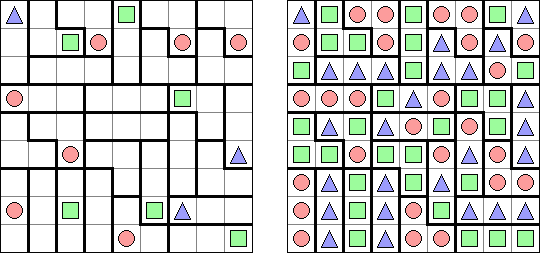
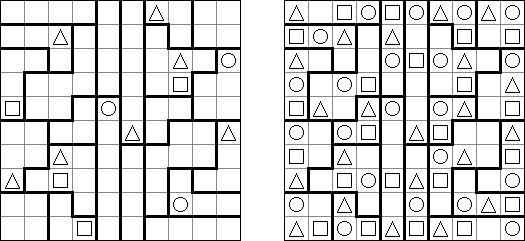
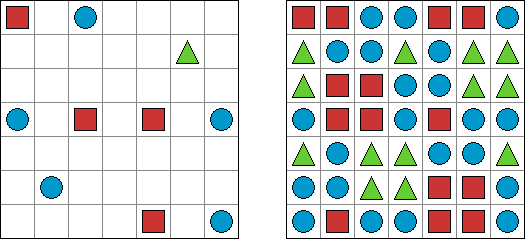
Triplets ("One or All") is a logic puzzle published by Nikoli. The task consists of a rectangular or square grid divided into regions of exactly three cells. Some cells contain figures of 3 kinds: squares, circles, triangles. The goal is to fill in each cell with figures. Each region must contain all identical or all different figures. When two figures are orthogonally adjacent across a region boundary, the figures must be different.
Korekutokonekuto ("Correct Connection") is a logic puzzle created by Naoki Inaba (Japan). The task consists of white and black circles; some white circles may contain digits. The aim is to connect all white circles by horizontal and vertical lines. The lines must not cross other lines or black circles. The number of lines connected to the white circle must match the digit in that circle.
Doppelblock consists of a square grid. The goal is to blacken two cells in each row and each column. The remaining white cells must be filled with the digits from 1 to N-2, where N is the size of the puzzle's side. Each number appears once in every row and column. Numbers outside the grid show the sums of the numbers between two black cells in corresponding row or column.
Furisuri ("Free Three") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains circles in some cells. The goal is to locate some blocks in the grid, having the size of exactly three cells. Each block must contain one circle. It must be possible to move each block by one cell in at least one direction.
Yagit (from Japanese "Yagi to ookami"; literally "goat and wolf") is a logic puzzle published by Nikoli. The task consists of a rectangular or square grid with circles ("goats") and squares ("wolves") in some cells. The task is to divide the grid into regions. Each region must contain either goats or wolves (but not both) and must not be empty. The border lines of the regions start and end on the edges of the grid. Lines can only turn at black dots. Lines can cross each other except at black dots. Not all black dots must be used by border lines.
Purenrupu ("Pure Loop") is a logic puzzle created by Naoki Inaba (Japan). A rectangular or square grid contains black cells. The aim is to draw a single loop. The loop visits all white cells exactly once. The segments of the loop run horizontally and vertically between the centers of white cells.
Firumatto ("Fillmat") is a logic puzzle published by Nikoli. A rectangular or square grid contains digits in some cells. It is necessary to divide the grid into rectangular regions. Every region must be exactly one cell wide; the other side of the region has length from 1 to 4 cells. A cell with a number indicates the size of a region. Two regions of the same size must not be orthogonally adjacent. A grid dot must not be shared by the corners of four regions.
Nawabari ("Territory") is a logic puzzle published by Nikoli. The aim is to divide the grid into rectangular regions such that each region contains exactly one digit. The digit in the cell represents how many sides of the cell belong to the borders of the regions, including the edge of the grid.
Makaro is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. Each region must be filled with each of the digits from 1 to the number of cells in the region. The grid may contain the black cells with arrows. The arrow points at the biggest number among the four cells around (up, under, left, right) the black cell. When two numbers are orthogonally adjacent across a region boundary, the numbers must be different.
Dosun-Fuwari is a logic puzzle published by Nikoli. The task consists of a grid divided into regions. The grid may contain black cells; black cells do not belong to any region. The aim is to place one black circle and one white circle in each region according to the following rules:
Satogaeri (from Japanese; literally "coming home") is a logic puzzle invented by Nikoli. A rectangular or square grid is divided into regions. Some cells of the grid contains circles (empty or with numbers). The task is to move the circles vertically or horizontally, so each region contains only one circle. The numbers in the circles indicate how many cells they have to pass through. Circles without numbers may move any distance, but some of them stay put. The circles cannot cross the tracks of other circles and cannot move over other circles.
Koburin is a logic puzzle published by Nikoli. A rectangular or square grid contains numbers in some cells. The aim is to blacken some cells and draw a single continuous non-intersecting loop that properly passes through all empty white cells. The number in the cell indicates the total number of black cells orthogonally adjacent to this cell. The grid may contain black cells not adjacent to cells with numbers. Cells with numbers must not be blacken. Two black cells must not be orthogonally adjacent.
Sukrokuro combines the elements of three logic puzzles: Sudoku, Kropki Sudoku and Kakuro. It consists of a square grid with white and black cells. The goal is to fill in the white cells, one number in each, so that each column and row contains the numbers 1 through 9 exactly once. Black cells contain a diagonal slash from top left to bottom right with numbers in them, called "the clues". Such number tells the sum of numbers in consecutive cells at its right or downward. If absolute difference between two numbers in neighboring cells equals 1, then they are separated by a dot. If a dot is absent between two white cells, the difference between the numbers in these cells is more than 1.
Shirokuro is a logic puzzle invented by Nikoli. It contains white and black circles. The task is to connect each white circle with a black circle by a horizontal or vertical line. Lines are not allowed to cross other lines. The line between two circles may not pass through other circles.
Roma is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. Some cells of the grid contains black circles. The goal is to place arrows pointing in four directions in each empty cell. Each region must contain all different arrows. Starting with any cell, following the arrows from cell to cell, this path must end in the cell with the black circle.
Bodaburokku ("Border Block") is a logic puzzle published by Nikoli. A rectangular or square grid contains numbers in some cells. It is necessary to divide the grid into regions. Cells with the same number belongs to the same region. All points where three or four lines meet are given. Every region contains at least one cell with a number.
Kuroshuto ("Kurochute"; from Japanese, literally "black shot") is a logic puzzle invented by Nikoli. A rectangular or square grid contains numbers in some cells. The goal is to blacken some empty cells. A cell with a number indicates that only one of the cells with such distance must be blackened. Two black cells must not be orthogonally adjacent. All of the white cells must be connected.
Toichika is a logic puzzle published by Nikoli. The task consists of a rectangular or square grid divided into regions. The goal is to place arrows in some cells according to the following rules:
Usotatami is a logic puzzle published by Nikoli. A rectangular or square grid contains numbers in some cells. The aim is to divide the grid into rectangular regions such that each region contains exactly one number. Every region must be exactly one cell wide; the length of the other side is NOT equal to the number in this region. A grid dot must not be shared by the corners of four regions.
Pipelink consists of a rectangular or square grid. The task is to draw a single continuous loop that passes through all cells. The loop must use all given sections and may cross itself in any cell.
Hakoiri is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. The goal is to place exactly one triangle, one square and one circle in each region. The same figures cannot be placed in adjacent cells, not even diagonally. All the figures must be connected horizontally or vertically.
Nuribou is a logic puzzle invented by Nikoli. A rectangular or square grid contains numbers in some cells. The task is to blacken some empty cells according to the rules:
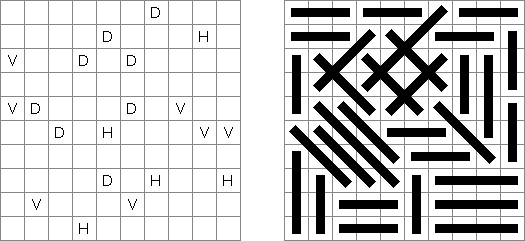
Tatamibari is a logic puzzle invented by Nikoli. A rectangular or square grid contains 3 kinds of symbols: cross, horizontal bar, vertical bar. The goal is to divide the grid into rectangular regions. Each region contains one cell with a symbol. A region with a cross must be a square. If a region contains a horizontal bar, the region's width must be greater than its height. If a region contains a vertical bar, the region's width must be less than its height. A grid dot must not be shared by the corners of four regions.
Sun and Moon ("Munraito") is a logic puzzle invented by Naoki Inaba (Japan). A square grid contains planets in some cells. The goal is to place exactly one star and one stardust cloud into each row and each column of the grid. If a particular semicircle of a planet is illuminated, there must be a star in that rank to light it. A star shines horizontally and vertically only; planets and stardust clouds block starlight.
Kojun is a logic puzzle invented by Nikoli. A rectangular or square grid is divided into regions. Some cells contain numbers. Each region must be filled with each of the digits from 1 to the number of cells in the region. When two numbers are orthogonally adjacent, the numbers must be different. The upper number of two vertically adjacent numbers in the same region must be greater than the lower number.
Usowan (from Japanese, literally "one liar") is a logic puzzle published by Nikoli. A grid is divided into rectangular and square regions. Some of the cells in the grid are numbered. The aim is to blacken some cells of a grid according to the following rules:
Gokigen Naname (from Japanese, literally "to be in a bad mood"; also known as "Slalom", "Slant") is a logic puzzle invented by Nikoli. It is played on a rectangular or square grid. Circles with digits from 0 to 4 may be situated on intersections of lines inside the grid. The aim is to fill in a diagonal line in every cell. The number in each circle equals the number of lines extending from that circle. The diagonal lines must not form a closed loop.
Hebi-Ichigo is a logic puzzle invented by Nikoli. The goal is to insert the numbers 1 to 5 according to the rules:
Hamle (from Turkish, literally "move") consists of a rectangular or square grid. The aim is to move every numbered black cell in one of the four directions, so that numbers in the cells indicate the length of their moves. When all moves are done, all white cells should be interconnected and numbered cells should not share an edge.
Gyokuseki (from Japanese, literally "gems and stones") is a logic puzzle created by Naoki Inaba (Japan). The aim is to fill a square grid with black circles ("gems") and white circles ("stones"). Every row and every column contains one black circle and random quantity of white circles. A number at the edge of the puzzle indicates how many circles can be seen in the corresponding row or column up to and including the black circle.
Kin-Kon-Kan is a logic puzzle published by Nikoli. The task consists of a rectangular or square grid divided into regions. The goal is to fill in some cells with diagonal lines ("mirrors"). Each region contains exactly one mirror. Letter-number pairs at the edges of the grid can be connected by straight lines ("laser beams") that bounce of the same number of mirrors as the number in the letter-number pair. Every mirror must reflect at least one laser beam.
Ichimaga is a logic puzzle invented by Nikoli. The task is to connect all circles by horizontal and vertical lines. The number of lines connected to the circle must match the digit in that circle. Any number of lines may be connected to the empty circle (at least one). The lines must not cross other lines. The line may change direction 90 degrees no more than once.
Shimaguni is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. The goal is to blacken some cells of a grid according to the following rules:
Meadows is a logic puzzle. It is played on a rectangular or square grid. Some of the cells have circles in them. The aim is to divide the grid into square blocks such that each block contains exactly one circle.
Yajisan-Kazusan (from Japanese, literally "arrow - number") is a logic puzzle published by Nikoli. The aim is to blacken some cells according to the following rules:
Snake Pit consists of a rectangular or square grid. The goal is to divide the grid into regions ("snakes") according to the following rules:
Hiroimono ("Goishi Hiroi"; from Japanese, literally "things picked up") is a logic puzzle invented by Nikoli. The grid contains circles ("stones") placed at some grid points. The task is to move along the grid lines and collect all the stones (number them in the order in which you pick them up) according to the following rules:
Water Fun ("Aquarium") is played on a rectangular or square grid. The goal is to fill water in some parts of the grid. Numbers outside the grid show how many cells of each row and column must be filled with water. Connected areas of filled cells must have the same level of water everywhere, like in a series of tubes.
Round Trip is a kind of logic puzzles. The aim is to draw a single loop in a rectangular or square grid. A loop may cross itself orthogonally, but otherwise does not touch or retrace itself. The numbers along the edge of the puzzle indicate the number of cells visited by the nearest section of the loop in corresponding row or column.
Number Cross consists of a square grid with numbers. The goal is to blacken some cells. Numbers outside the grid show the sums of the numbers in white cells in corresponding row or column.
Santoitchi (from Japanese, literally "three and one") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains numbers in some cells. The task is to blacken some empty cells according to the rules:
Hamusando ("Ham Sandwich") is a logic puzzle invented by Naoki Inaba (Japan). The goal is to fill a square grid with squares ("toasts") and circles ("pieces of ham"). Every row and every column contains two squares and N circles (N is given for each puzzle). A number at the edge of the grid indicates how many circles must be placed between the two squares in the corresponding row or column.
Trace Numbers consists of a rectangular or square grid with numbers in some cells. The aim is to draw as many lines into the grid as it contains cells with the number 1. The line may only travel horizontally or vertically, and never diagonally. The line starts in the cell with the number 1 and visits all cells with numbers in order through the highest number. Each cell must be visited exactly once; lines cannot cross.
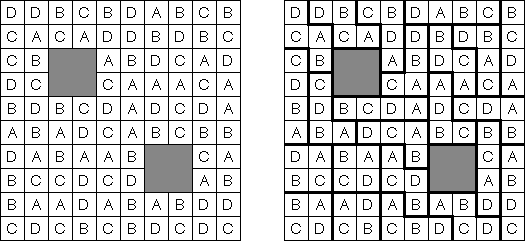
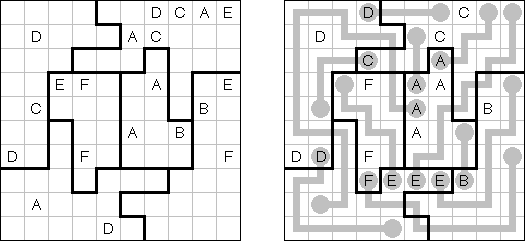
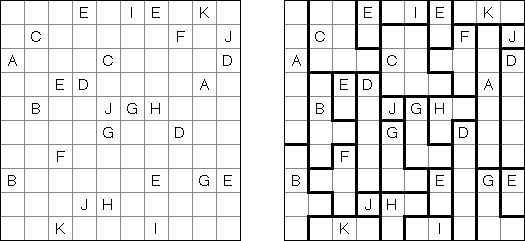
Area Division is played on a grid filled with Latin letters. The goal is to divide the grid into regions. Each region has all the letters of the given range. The region contains each letter exactly once. Each letter must be part of exactly one region.
Sukoro consists of a rectangular or square grid with numbers from 1 to 4 in some cells. The number inside a cell represents how many neighbouring cells contain numbers. When two cells with numbers are orthogonally adjacent, the numbers must be different. All the cells with numbers must be connected horizontally or vertically.
EntryExit consists of a rectangular or square grid divided into regions. The aim is to draw a single continuous non-intersecting loop that passes through all cells. It can enter and exit each region only once.
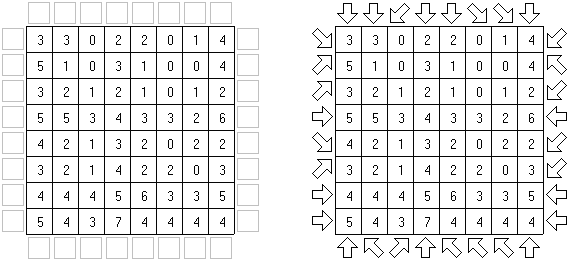
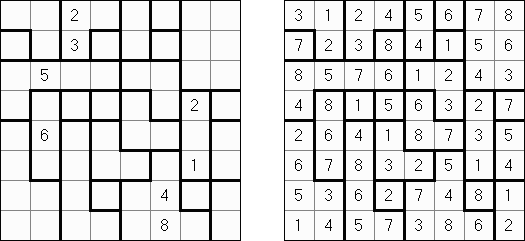
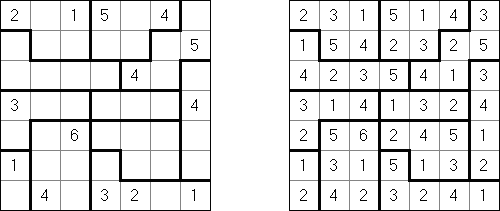
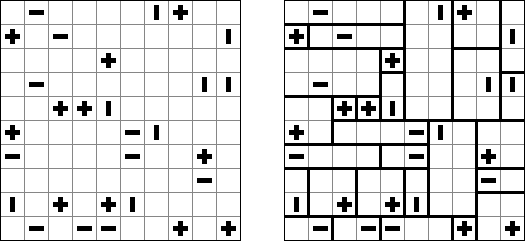
Sign In is played on a square grid. The goal is to fill in each cell with numbers from 1 to N, where N is the size of the puzzle's side. No number may appear twice in any row or column. Some digits may be given at the start. If absolute difference between two digits in neighboring cells equals 1, then they are separated by a sign "+" or "-". If a border between cells contains a sign "+", a digit in a left or upper cell is one lower than a digit in a right or lower cell. If a border between cells contains a sign "-", a digit in a left or upper cell is one bigger than a digit in a right or lower cell. All instances of consecutive digits are shown by these signs.
Kuroshiro ("Kuroshirorupu"; from Japanese, literally "black and white loop") is played on a grid with black and white circles in some cells. The goal is to draw a single continuous non-intersecting loop that properly passes through all circled cells. Between two successive circles of the same color the loop must not be turned. Between two successive circles of different colors the loop must turn exactly once.
Moonsun ("Moon or Sun") is a logic puzzle invented by Nikoli. A rectangular or square grid is divided into regions. A grid contains black and white circles in some cells. The aim is to draw a single non-intersecting loop. The loop must cross borders of each region exactly twice. In a region the loop must visit either all cells with black circles or all cells with white circles. Regions with visited black circles must alternate with regions, where white circles were visited.
Rectslider ("Rectangle-Slider", "Shikaku suraida") consists of a rectangular or square grid with black cells. The task is to move the black cells vertically or horizontally, so black cells form rectangles having area greater than one cell. Two black rectangles must not be orthogonally adjacent. The numbers in the black cells indicate how many cells they have to pass through. Black cells without numbers may move any distance, but some of them stay put. The black cells cannot cross the tracks of other black cells and cannot move over other black cells.
Stostone ("Sto-Stone", "Stone on Stone") is a logic puzzle invented by Nikoli. A rectangular or square grid is divided into regions. The goal is to blacken some cells of a grid ("stones") according to the following rules:
Kohi Gyunyu (from Japanese, literally "coffee milk") consists of white, black and gray circles. The aim is to connect circles by horizontal and vertical lines. All connected circles form a group. Each group must contain exactly one gray circle and equal amounts of white and black circles. The lines must not cross other lines. White and black circles cannot be directly connected.
Mirukuti ("Milk Tea", "Milk-T") consists of a rectangular or square grid with black and white circles in some cells. The goal is to connect each group of three circles (one black cell and two white circles) by a T-shaped line. Two white circles must be connected by the straight-line segment of the T-shaped line. The lines must not cross other lines.
Slash Pack is a logic puzzle invented by Yosuke Imai (Japan). The grid of irregular shape contains numbers from 1 to N in some cells. The goal is to divide the grid into regions by placing the diagonal lines into empty cells. Each region must contain the numbers from 1 to N exactly once. Two diagonals cannot cross in one cell, and there can be no loose ends.
Nurimaze ("Nurimeizu") consists of a grid divided on regions. The aim is to blacken some regions according to the following rules:
Canal View is played on a rectangular grid. Some of these cells have numbers in them. The aim is to blacken some cells of a grid according to the following rules:
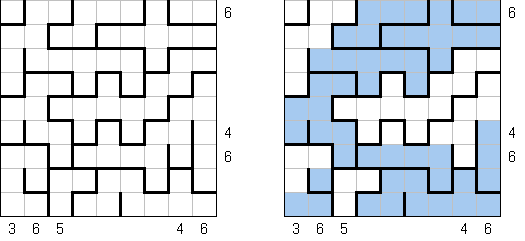
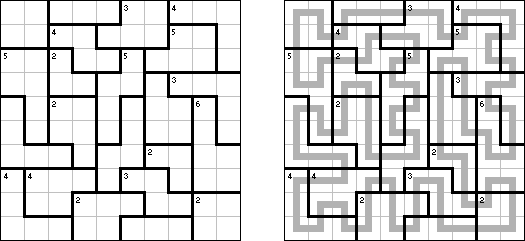
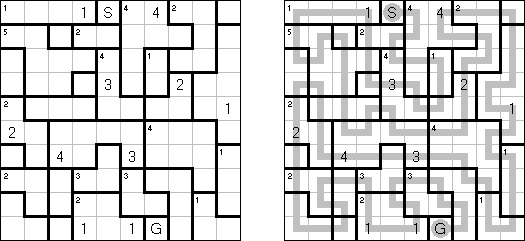
Country Road is a logic puzzle invented by Nikoli. The puzzle consists of a rectangular grid of any size divided into regions. The goal is to draw a single continuous non-intersecting loop that connects the centers of the grid cells. The loop must visit each region exactly once. The number in a region indicates how many cells of this region are visited by the loop. In regions without a number the loop may visit any number of cells. If the loop does not visit any two neigbouring cells, these cells must be in the same region.
Nondango (dango is a Japanese dish, small balls made from rice flour and skewered on bamboo sticks) is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. Each region contains circles in some cells. The aim is to blacken some circles according to the following rules:
Mintonette (the original name of the game known as volleyball) is played on a grid of irregular shape with circles in some cells. The goal is to connect circles in pairs by drawing a line that goes horizontally and vertically through the centers of cells. Lines cannot touch or cross themselves or each other. If a circle contains a number, it represents the number of turns for the line between two circles. If two circles have no number, a line may make any number of turns between circles. All cells must be used by the lines, and each circle must be connected to another circle.
Arrow Maze consists of a rectangular or square grid with arrows. The aim is to find a path through the grid by visiting every cell once. The path is starting from the cell with number 1. The path can jump from one cell to another in a horizontal, vertical or diagonal direction, but only in the direction of the arrow. Some numbers have already been given.
Arrow Web is a logic puzzle. A rectangular or square grid is filled by arrows. The goal is to shade some of the arrows so that each arrow in the grid points to exactly one shaded arrow.
Hanare ("Hanaregumi"; from Japanese, literally "family pair") is a logic puzzle. A square or rectangular grid is divided into regions. The aim to place a number into each region. A number is equal to the size of the region. The distance between two horizontally or vertically neighboring numbers must be equal to the difference of these numbers.
Oases is a logic puzzle. A rectangular or square grid contains circles with numbers in some cells. The goal is to blacken some cells (leaving the other cells white) so that the unshaded cells must be connected horizontally or vertically. Blackened cells should not share an edge. Cells with circles cannot be blackened. Unshaded cells must not cover an area of size 2 x 2. Each circled number represents the number of other circles that can be reached from that circle by only going through empty (unshaded and uncircled) cells. (A circle that can be reached by more than one path still only counts as one circle for counting purposes.)
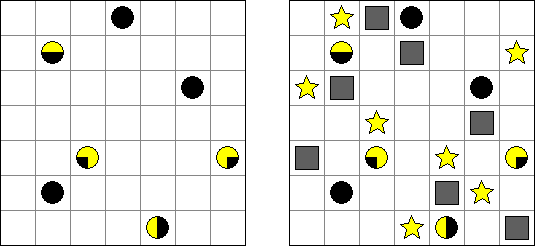
Rabbits and Trees (also known as "Raitonanba", "Light Number") is a square grid with numbers in some cells. The task is to place exactly one white circle ("rabbit") and one black circle ("tree") in every row and every column. A number indicates how many white circles ("rabbits") can be seen in the corresponding row and column. A rabbit is visible only when it is not hidden behind a tree.
Stars and Arrows consists of a rectangular or square grid with arrows in some cells. The aim is to place stars in empty cells. Each arrow points to exactly one star and each star is pointed by exactly one arrow. Numbers outside the grid show the numbers of stars in corresponding row or column.
Kanjo ("Kanjo-sen supesharu"; from Japanese, literally "special ring line") is a logic puzzle. A rectangular or square grid contains circles with numbers in some cells. The goal is to draw loops that properly passes through all cells. A loop may cross itself or other loops. All given line fregments must be used as a part of a loop. Cells with the same number belong to the same loop. Cells with different numbers belong to different loops. A loop must go trough at least one cell with a number (there are exactly as many loops as a grid contains different numbers). A cell with a number must not contain the intersection point where a loop crosses itself or other loop.
Rukkuea ("Look-Air") is a logic puzzle invented by Nikoli. The puzzle consists of a rectangular or square grid with numbers in some cells. It is necessary to blacken some cells according to the following rules:
Golem Grad (an island in Lake Prespa, in the Republic of North Macedonia) combines the rules of Nurikabe and Snake puzzles. A rectangular or square grid contains circles and numbers in some cells. The aim is to blacken some cells according to the following rules:
Trilogy consists of a square or rectangular grid with figures in some cells: squares, circles, triangles. The goal is to fill in each cell with figures. Three consecutive figures must not be all the same and must not be all different in any row, column or diagonal.
Grades is a logic puzzle. The goal is to place numbers in some cells of a square or rectangular grid according to the rules:
Hukuwall is a logic puzzle created by Nishiyama Yukari (Japan). A rectangular or square grid contains letters in some cells. The goal is to draw a horizontal or vertical line in every empty cell. Each letter stands for a number: all the same letters must be replaced by the same number, different letters must be replaced by different numbers. A number in a cell indicates the total length of the lines that end at the edges of this cell. A line cannot connect two cells with letters. The numbers of line directions coming out of the same letter are all different.
Nurimisaki (from Japanese, literally "paint a cape") is a logic puzzle invented by Nikoli. A rectangular or square grid contains circles in some cells; a circle may have a number inside or not. The task is to blacken some cells of a grid according to the following rules:
Starry Night ("Niapuresu", "Near Place") is a logic puzzle invented by Naoki Inaba (Japan). The aim is to place one white circle ("sun"), one black circle ("moon") and one star in every row and column of the grid. Same figures may not touch each other diagonally. The figures outside the grid indicate the distance between the star and circles in that row or column:
Douieru (from Japanese, literally "same and different") is a logic puzzle invented by Nishiyama Yukari (Japan). A rectangular or square grid contains circles in some cells. The aim is to divide the grid into L-shaped regions. The two "legs" of a region must be exactly one cell wide. A circle represents a cell in which an "L" must bend (the grid contains circles for all regions). If a cell contains a double circle, the two legs of the region must have the same length. A black circle means difference in leg lengths. If a cell contains a white circle, the ratio of leg lengths is unknown.
Tetoron is a logic puzzle invented by Nishiyama Yukari (Japan). A rectangular or square grid contains symbols in some cells. The goal is to divide the grid into regions of exactly four cells (tetromino). Each region contains exactly two different symbols. Regions of the same shape must contain the same symbols. The tetrominoes may be rotated or mirrored.
Sashikaku (from Japanese, literally "square by difference") is a logic puzzle created by Nishiyama Yukari (Japan). A rectangular or square grid contains numbers in some cells. The aim is to divide the grid into rectangular and square regions such that each region contains exactly one number, and that number represents the difference of the width and height of the region.
Heki is a logic puzzle invented by Nishiyama Yukari (Japan). A rectangular or square grid contains numbers in some cells. The goal is to divide the grid into regions of exactly six cells. Each region contains exactly two numbers. The number indicates how many cells of the same region are orthogonally adjacent to the cell with the number.
Castle Wall is a logic puzzle created by Palmer Mebane (USA). A rectangular or square grid contains black or bordered cells; some of them contains numbers and arrows. The aim is to draw a single closed non-intersecting loop. Black cells must be outside the loop; white bordered cells must be inside the loop. Numbers and arrows refer to the total length of loop segments in the arrow's direction. (In other words, the number shows how many cell borders in the arrow's direction are crossed by the loop.)
Deddoanguru ("Dead Angle") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains black circles with numbers. The aim is to divide the grid into regions. Each region contains one black circle. A black circle is an eye that looks in all four directions until a region border. The number in the cell represents how many cells of the region the eye does not see.
Endorain ("End Line") is a logic puzzle created by Naoki Inaba (Japan). A rectangular or square grid is divided into regions. The goal is to draw horizontal and vertical lines between the centers of cells. Each line connects two cells in different regions. A number in a region indicates how many lines start/end in this region. All cells must be used by the lines.
Nuraf (also known as "Araf Nurikabe") combines the rules of Nurikabe and Araf puzzles. A rectangular or square grid contains numbers in some cells. The aim is to blacken some cells of a grid according to the following rules:
Miti (from Japanese, literally "road") is a logic puzzle created by Nishiyama Yukari (Japan). A rectangular or square grid contains dots at some intersections of the grid lines. The goal is to blacken some borders between cells. In each given grid dot exactly three black lines must meet. In all other grid dots at most two black lines may intersect. All cells of the grid form a single closed loop without dead ends, exactly one cell wide.
Arofuro ("Arrow Flow") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains numbers in some cells. The aim is to place arrows pointing in four directions in each empty cell.
Every Second Turn (also known as "Alternate Corners", "Every Second Breakpoint") is a rectangular or square grid with circles in some cells. The aim is to draw a single continuous non-intersecting loop that visits every cell exactly ones. It makes a 90 degrees turn at every cell with a circle. There is exactly one turn between two consecutive circles that the loop visits.
Mobiriti ("Mobility") is a logic puzzle created by Naoki Inaba (Japan). A rectangular or square grid contains circles with numbers in some cells. The aim is to blacken some cells of a grid. Cells with circles can not be blacken. A number in a circle indicates how many empty white cells can be reached from that cell by moving horizontally or vertically.
Mubunanba ("Move Number") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains digits in some cells. The goal is to locate some blocks in the grid, having the size of exactly three cells. The grid may contain cells that belong to no one block. Each block contains exactly one digit. A digit indicates the number of the possible directions to move a block.
Terra X consists of a rectangular or square grid divided into regions. The aim is to place a digit from 0 to 9 into each region so that regions with equal numbers cannot share an edge (they may touch each other diagonally). For each grid point where four regions meet, the sum of the digits in those regions must equal 10. (All these grid points are marked with a small black dot.)
Rimotoejji ("Remote Edge") is a logic puzzle created by Naoki Inaba (Japan). The goal is to connect all dots by a single continuous non-intersecting loop. All arrows and crosses are supposed to be contained within the loop. An arrow points in the direction of the longest straight sequence of cells visible from that cell. A cross is placed at the center of more than one longest straight sequences of cells within the loop.
Double Back consists of a rectangular or square grid divided into regions. The aim is to draw a single closed loop of horizontal and vertical segments passing through all white cells. Each region must be visited exactly twice. The grid may contain black cells; the loop cannot pass through a black cell.
Wamuzu ("Worms") is a logic puzzle invented by Naoki Inaba (Japan). It consists of a grid, with circles in some cells. The goal is to connect circles in pairs by drawing a line that goes horizontally and vertically through the centers of cells. All cells must be used by the lines. All sections of each line must be equal to the length of the cell's side.
Kaero ("Ouchihekaero"; from Japanese, literally "let's go home") is a logic puzzle created by Naoki Inaba (Japan). A rectangular or square grid is divided into regions. The aim is to move some letters horizontally or vertically, so all letters in a region must be the same. The letters cannot cross the tracks of other letters and cannot move over other letters.
Kapama (from Turkish, literally "closing") consists of a rectangular or square grid with diagonal lines in some cells. The goal is to blacken some cells to create pairs of figures (twin shapes). Twin shapes are symmetrical with respect to a diagonal line. Twin shapes are connected with a diagonal line. No two shapes may share an edge. Cells with diagonal lines can not be blacken. Numbers outside the grid show the number of black cells in corresponding row or column.
Yunikumaka ("Unique Marker") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains dots; a dot can be situated in the center of a cell or on a border between neighbouring cells. The aim is to divide a grid on regions having the size of exactly four cells (tetromino). Each region contains exactly one dot either in the center of a cell or on a border between cells. Dots on borders between regions are ignored. Black cells do not belong to any region.
Meandering Numbers (also known as "Count Number", "Worms") is played on a rectangular or square grid divided into regions. A grid may contain numbers in some cells. Each region must be filled with each of the digits from 1 to N, where N is the number of cells in the region. Cells with the same digits must not be orthogonally or diagonally adjacent. Consecutive numbers within the region are orthogonally adjacent. (For each region it must be possible to draw a path that starts at 1 and ends at N, going through each other cell exactly once and in numerically increasing order.)
Yokibunkatsu (from Japanese, literally "container dividing") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains stars in some cells. The goal is to divide the grid into regions of exactly five cells. Each region contains a star. The cells of the region must be foldable to a cube, with the star at the bottom and without the top side ("roof"). Some sections of borders between regions have already been given. The grid may contain cells that belong to no one region.
Scrin ("Screen") is a logic puzzle published by Nikoli. A rectangular or square grid contains circles (empty or with numbers) in some cells. The goal is to divide the grid into rectangular regions. Each region contains not more than one circle. The grid may contain regions without circles. A region must have the same number of cells as a number in a circle. Regions must not share an edge. Regions must form a single non-branching loop where all of them touch each other by corners.
From 1 To X consists of a rectangular or square grid divided into regions. Each region must be filled with each of the numbers from 1 to the number of cells in the room. Same numbers must not be orthogonally adjacent. Numbers outside the grid show the sums of the numbers in corresponding row or column.
Shingoki (from Japanese, literally "traffic lights") is a rectangular or square grid with circles in some cells. The goal is to draw a single continuous non-intersecting loop that passes through all circles. Black circles must be turned upon, white circles must be traveled straight through. In a cell with a gray circle the loop may turn or not. If a circle contains a number, this number indicates the total length of the straight lines going out of the circle.
Stitches consists of a rectangular or square grid divided into regions. The aim is to connect each region with all neighbor regions with exactly one line ("stitch"). A length of each line is one cell (it connects two orthogonally adjacent cells from different regions). A cell may be visited at most one line. A number at the edge of the grid indicates how many line end points must be placed in the corresponding row or column. Cross+A can solve puzzles with 2, 3 or 4 lines connecting neighbor regions.
Neibadomino ("Neighbour Domino") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains numbers in some cells. The aim is to locate some blocks in the grid, having the size of exactly two cells ("dominoes"), and fill blocks with numbers. The grid may contain cells that belong to no one block. Each number in the grid should be part of a block, indicating the amount of orthogonally adjacent dominoes. Blocks with the same numbers must not be orthogonally adjacent. Blocks must not cover an area of 2 x 2 cells. (The grid may contain 2 x 2 cell area without blocks.)
Jemini ("Jemini Block") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains letters in some cells. The goal is to divide the grid into regions such that each region contains exactly one letter. In regions of the same size, shape and orientation the same letter must be exactly at the same position.
Double Choco is a logic puzzle published by Nikoli. In a rectangular or square grid exactly half of cells are painted gray. The aim is to divide the grid into regions. Each region must contain one area of white cells and one area of gray cells. A pair of areas must be of the same shape and size (the areas may be rotated or mirrored). A number indicates how many cells of the same color the region contains. A region may contain more than one cell with a number (in this case the cells contain the same number).
Konarupu ("Corner Loop") is a logic puzzle invented by Naoki Inaba (Japan). The goal is to create a continuous non-intersecting loop, drawn from one dot to an adjacent dot horizontally or vertically. A number in a cell indicates how many times the loop turns by 90 degrees in dots surrounding this cell.
Gaidoaro ("Guide Arrow") is a logic puzzle created by Naoki Inaba (Japan). A rectangular or square grid contains arrows and a single star. The goal is to blacken some cells so that the white cells must be connected horizontally or vertically. Blackened cells should not share an edge. Cells with arrows or a star cannot be blackened. An arrow indicates the direction in which you must move to reach a star by only going through white cells (there must be only one way from any white cell to reach a cell with a star).
Mid-Loop is a logic puzzle published by Nikoli. A rectangular or square grid contains dots; a dot can be situated in the center of a cell or on a border between neighbouring cells. The aim is to draw a single continuous non-intersecting loop that properly passes through all dots. Dots must be traveled straight through. Segments of a straight line going out of a dot must be equal.
Dotchi-Loop is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. A grid contains white and black circles in some cells. The goal is to draw a single non-intersecting loop. The loop must visit all cells with white circles; the loop cannot pass through a black circle. The line either travels straight through all the white circles, or makes a 90 degrees turn at all the white circles in a region.
Trinairo is a logic puzzle invented by Leo de Winter (Netherlands). The objective is to fill a 9 x 9 grid with letters so that each row and each column contains three letters A, three letters B and three letters C. If a cell is marked with other color, a letter in the cell differs from letters in all orthogonally adjacent cells.
Detour is a logic puzzle. It contains a rectangular or square grid divided into regions. The goal is to draw a single continuous non-intersecting loop that visits every cell exactly ones. Each number in a region indicates the number of times the loop turns in the region.
Balance Loop is a logic puzzle created by Prasanna Seshadri (India). A rectangular or square grid contains black and white circles in some cells. The aim is to draw a single continuous non-intersecting loop that visits all cells with circles. Loop segments extending from a white circle are of equal length, while the loop segments extending from a black circle are not. If a cirlce contains a number, it indicates the sum of the loop segment lengths on both sides of the circle.
Turf is a logic puzzle invented by John Bulten (USA). A rectangular or square grid contains numbers in some cells. The goal is to shade some cells so that the grid will be divided into gray and white regions. Each region must contain at least one number. This number indicates the size of a region. If a region contains any other cell with a number, it represents how many surrounding cells are white, including itself and diagonal ones.
SquarO is a logic puzzle similar to Minesweeper. A rectangular or square grid contains dots on intersections of lines. A number in a cell indicates how many of the four surrounding dots are black.
Chiyotsui (from Japanese, literally "door hinge") is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. The goal is to blacken some cells of a grid according to the following rules:
Aqre is a logic puzzle invented by Eric Fox (USA). A rectangular or square grid is divided into regions. The goal is to blacken some cells of a grid that all black cells form one orthogonally connected area. A cell with a number indicates how many cells in the region must be blackened. In regions without a number any amount of cells may be blackened (all cells may stay white). There cannot be a run of more than three black or white cells in the grid.
Geradeweg ("Straight Loop") is a logic puzzle. A rectangular or square grid contains circles with numbers in some cells. The task is to draw a single closed non-intersecting loop that passes through all circles. The number indicates the length of the straight segment passed through the circle. If the loop turns in a number cell, both straight segments must have the same length as the number indicates.
Kuroclone is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. The aim is to blacken some cells of a grid. Each region must contain two areas of black cells: this pair of areas must be of the same shape and size (the areas may be rotated or mirrored). Cells with numbers are always white. The arrow points to an adjacent cell that belongs to a black area. The number indicates the size of this area. When two cells are orthogonally adjacent across a region boundary, at least one cell must be white.
Yajisan-Sokoban is a logic puzzle invented by Jamie Hargrove. A rectangular or square grid contains gray squares. The task is to move the gray squares vertically or horizontally (some squares may stay unshifted). Gray squares cannot cross the tracks of other gray squares and cannot move over other squares (gray squares can pass through numbered cells). A cell containing a number and an arrow represents how many gray squares are in the row or column pointed at by the arrow. If there is a gray square on top of a numbered cell, it plays no further role in the puzzle, and may be true or false. If a gray square passes through a cell with a number and an arrow, this numbered cell provides true information.
Line Segment is a logic puzzle invented by Erich Friedman (USA). The task is to draw line segments that pass through exactly 3 or 4 consecutive cells. The line segments can only be horizontal (H), vertical (V), or diagonal (D). Each cell must be visited exactly once. A cell with a letter contains a line segment with that orientation.
Raneko ("Ranekomappu"; from Japanese, literally "cat habitat map") is a logic puzzle published by Nikoli. A rectangular or square grid contains circles (with numbers or empty). The goal is to divide the grid into regions. Each region contains one circle ("cat"). A circle with a number indicates the size of a region. A grid may contain black cells. The number in a black cell indicates how many regions share an edge with that black cell.
Factorism ("Find the Factors") is a logic puzzle invented by Iva Sallay (USA). The goal is to place numbers from 1 to N across the top and down the left of the square grid N x N. A number in a cell indicates the product of numbers outside the grid in the corresponding row and column.
Akiperago ("Archipelago") is a logic puzzle published by Nikoli. A rectangular or square grid contains black cells; some of them contains numbers. The goal is to blacken some cells of a grid according to the following rules:
Yakazu is a logic puzzle invented by Patrick Tirone. A rectangular or square grid is partially divided by black cells into compartments. The aim is to fill all white cells with the numbers. Each compartment, vertically or horizontally, must contain a set of consecutive numbers, but in any order (for example: 4-1-3-2). Each compartment of two cells or more must contain all the numbers starting from 1.
Miraringutairu ("Mirroring Tile") is a logic puzzle published by Nikoli. A rectangular or square grid contains black cells; some of them contain numbers. The goal is to locate blocks of black cells in the grid. Each numbered cell indicates the total number of black cells in the block (a block may contain few numbered cells). The grid may contain blocks without numbers. No two blocks may share an edge, but each block must be connected with at least one another block of the same size and shape through their corners (blocks may be rotated or mirrored).
Heyablock ("Heyawake-Block") is a logic puzzle invented by Atsumi Hirose (Japan). A rectangular or square grid is divided into regions. The aim is to blacken some cells of a grid according to the following rules:
Choco Banana is a logic puzzle published by Nikoli. A rectangular or square grid contains numbers in some cells. The goal is to blacken some cells of a grid. An area of black cells must form a rectangle or square. An area of white cells must not form a rectangle or square. If a black or white area contains a number, it indicates the size of this area. An area may contain more than one cell with a number.
Wataridori (from Japanese, literally "migratory birds") is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. A grid contains circles (empty or with numbers) in some cells. The aim is to connect circles in pairs by drawing a line that goes horizontally and vertically through the centers of cells. A cell may be visited by a line at most once. A line may connect circles with equal numbers, empty circles, or a line may be drawn between an empty circle and a circle with a number. A number in a circle indicates how many regions are visited by the line. A region may be visited by the line at most once.
Chenburo ("Chain Block") is a logic puzzle published by Nikoli. A grid contains numbers or question marks in some cells. The aim is to blacken some cells of a grid according to the following rules:
Wanrumuwandoa ("One Room One Door") is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions ("rooms"). A region may contain a cell with a number. The goal is to blacken some cells of a grid according to the following rules:
Haisu ("House") is a logic puzzle invented by William Hu. A square or rectangular grid is divided into regions. The aim is to draw a line ("path") from S (start) to G (goal) that goes through all cells. The line cannot cross itself. The line can visit each region more than once. When the line passes over a cell with a big number N, it is on its Nth entry to the region. If a region has a small number n in the top left corner, the line must visit this region a total of n times.
Obitaru (from Japanese, literally "orbital") is a logic puzzle published by Nikoli. A grid contains white and black circles; black circles may contain numbers. The goal is to draw square or rectangular loops ("belts"). The loops may cross each other, but parallel lines cannot pass through the same cell. Loops must pass through all white cells. There may be loops that do not pass through any white circle. A black circle should be inside exactly one loop (there can be no more than one black circle inside the loop). If the black circle contains a number, it will be equal to the number of white circles through which the loop passes around this black circle.
Square Jam is a logic puzzle. A rectangular or square grid contains numbers in some cells. The aim is to divide the grid into square regions. A cell with a number indicates the side length of a region. A region may contain any amount of numbered cells. The grid may contain regions without numbers. A grid dot must not be shared by the corners of four regions.
Cocktail Lamp ("Kakuteruranpu") is a logic puzzle. A rectangular or square grid is divided into regions. The goal is to blacken some cells of a grid according to the following rules:
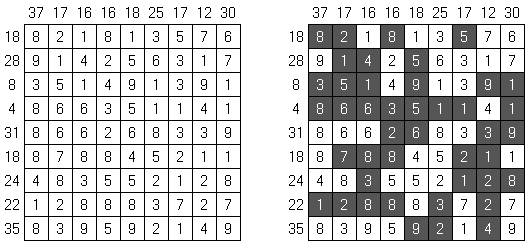
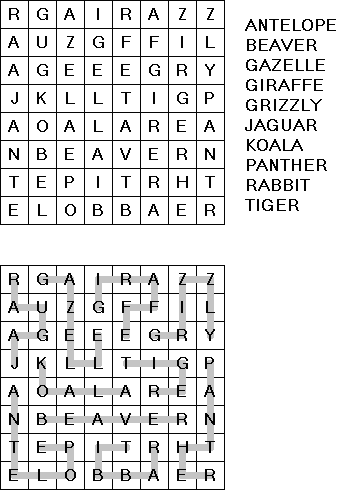
单词的谜题 Word Finder("单词搜索", "Word Search","Word Seek","Word Sleuth","Mystery Word")使用正方形或长方形的格网,里面有字母。需要在格网中找单词。单词的字母要用折线连接起来;这条线只弯曲90度。每一个字母只能使用一次。 为了制作谜题,先需要选择单词。而且,也可以选择关键词,解完谜题以后,未使用的字母就构成关键词。
Nine Letters - 是 Word Finder 单词的谜题的变种。使用正方形的格网,分为小格(3×3),里面有字母。需要在格网中找9个字母的单词。
Spider Web - 有被一条线连接起来的圈儿。在圆圈中有字母。需要找包括关键单词字母的圈儿的连续序列。
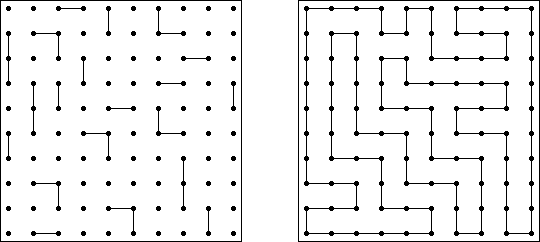
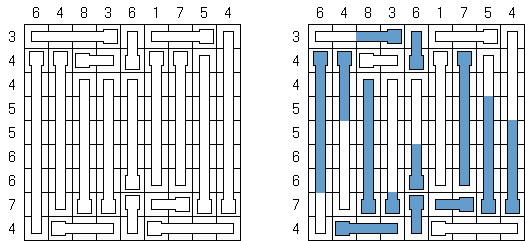
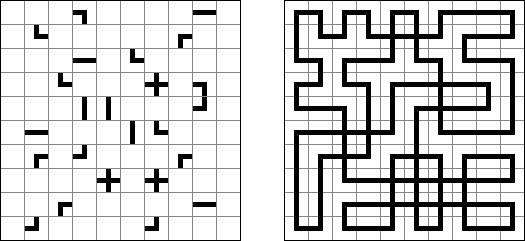
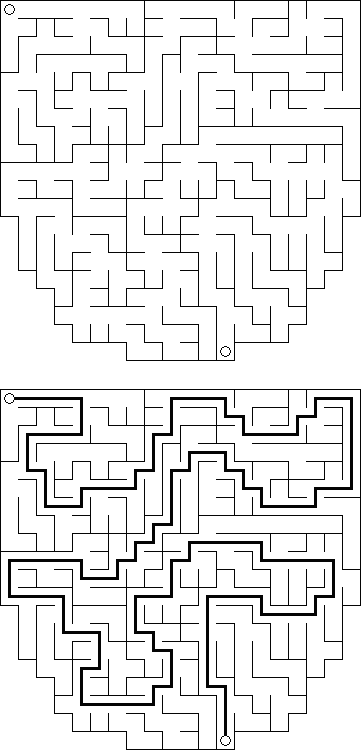
其他的游戏 Maze (迷宫) - 是一个错综复杂的道路组成的结构。需要找到两个标出的点之间的路径。计算机程序使您可以创建任意形状的迷宫,不仅是长方形或正方形。
|